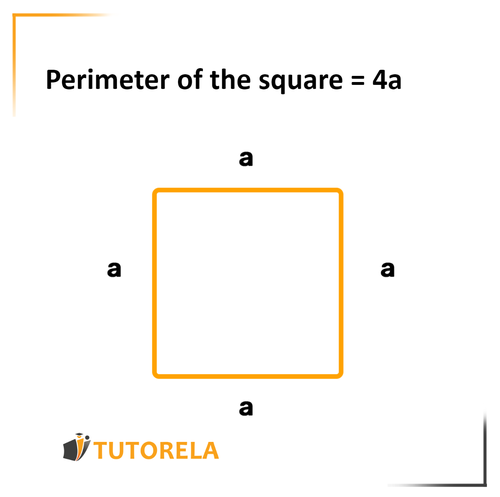
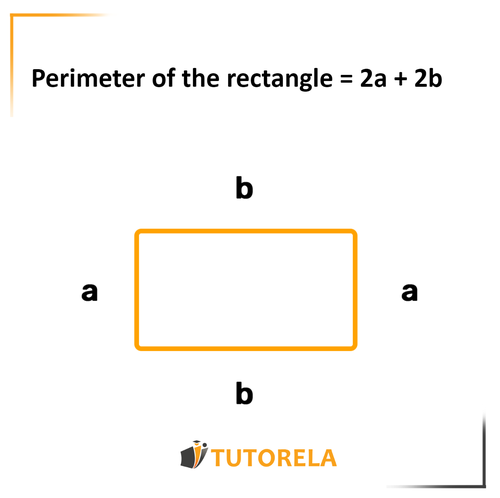
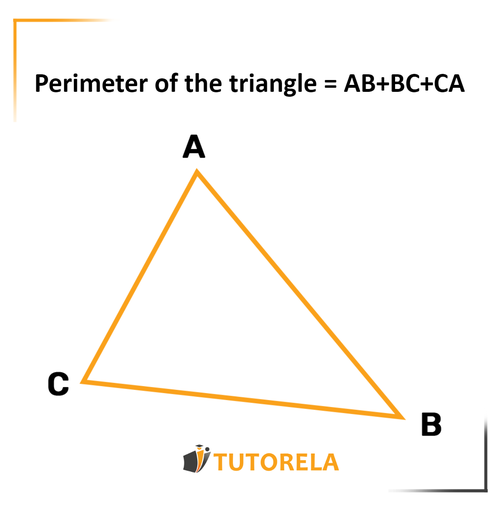
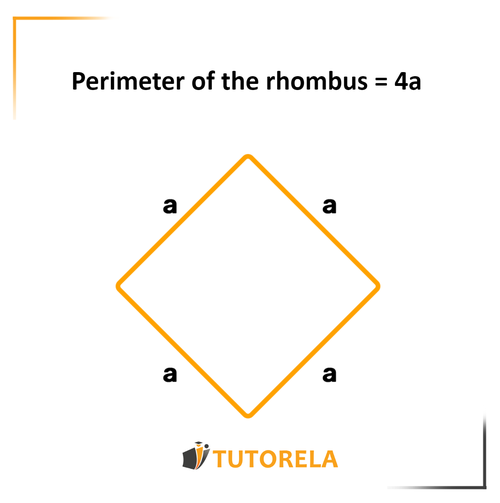
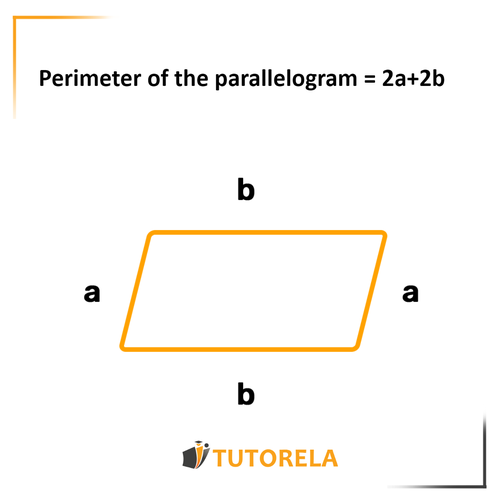
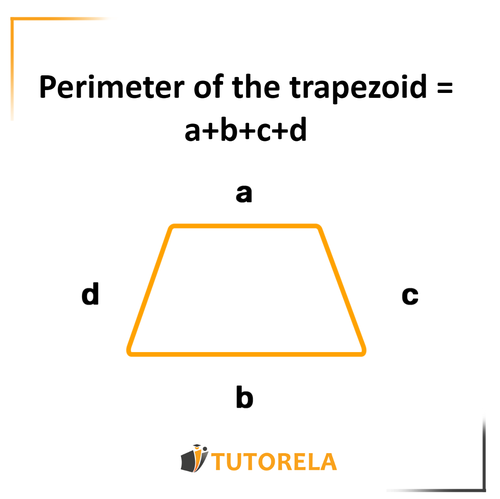
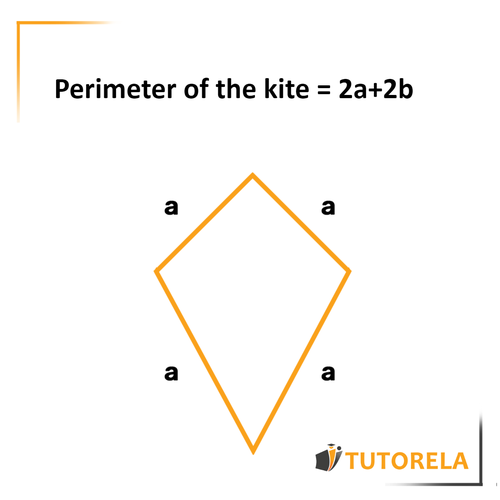
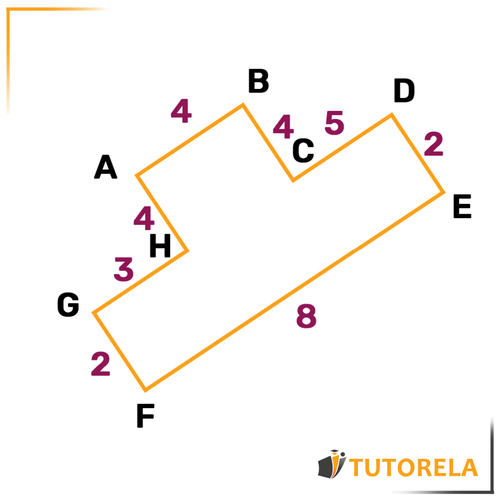
The perimeter indicates the distance we will walk if we start from a certain point, complete a full lap, and return exactly to the starting point. For example, if we are asked what the perimeter of the waist is, we will take a tape measure and measure the perimeter from a certain point until completing a full lap and returning to the same point from which we started the measurement. It works exactly the same way in mathematics. The perimeter of any shape is the distance from a specific point back to it after having completely surrounded it. If this is our figure:
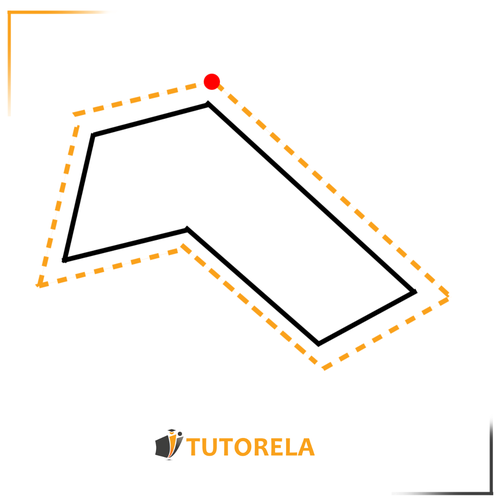
Its perimeter will be the distance we cover if we travel along its line from a certain point, and return to it after making a full lap. Imagine that you are surrounding the figure:
The perimeter is measured in units of mm, cm, or meters, according to what the question states. Generally, most figures are given in units of cm. We can convert the different units of measure in the following way: 1 cm = 10 mm 1 meter = 100 cm
Now we will learn to calculate the perimeter of the most known figures. Are we ready? How is the perimeter calculated in general? All the lengths of the edges (or sides) of the figure are added together. The sum of all the edges is the perimeter.
Perimeter of the Square
a -> Side of the square In the square, all sides are equal, therefore, its perimeter will be 4 times the side a. We will multiply the side of the square by 4.
Join Over 30,000 Students Excelling in Math!
Endless Practice, Expert Guidance - Elevate Your Math Skills Today
Test your knowledge
Question 1
Look at the rectangle below.
Side AB is 4.8 cm long and side AD has a length of 12 cm.
Let's add up all the sides of the triangle. In an isosceles triangle it is enough to know the length of the base and one of the two equal sides. In an equilateral triangle it is enough to know the length of one side.
The key to calculating the perimeter of these figures is to add up absolutely all the sides without forgetting any of them. Start on one side, follow the entire round and stop when you reach the same side from which you started.
What is the difference between perimeter and surface area?
The perimeter is measured in two-dimensional figures that do not have volume, for example, a rectangle
In contrast, the surface area is measured in three-dimensional figures that do have volume, for example, a cylinder or cube.
Examples and exercises with solutions for the perimeter of the parallelogram
Exercise #1
Look at the rectangle below.
Side AB is 2 cm long and side BC has a length of 7 cm.
What is the perimeter of the rectangle?
Video Solution
Step-by-Step Solution
Since in a rectangle every pair of opposite sides are equal to each other, we can claim that:
AB=CD=2
AD=BC=7
Now we can add all the sides together and find the perimeter:
2+7+2+7=4+14=18
Answer
18 cm
Exercise #2
Look at the rectangle below.
Side AB is 4.8 cm long and side AD has a length of 12 cm.
What is the perimeter of the rectangle?
Video Solution
Step-by-Step Solution
In the drawing, we have a rectangle, although it is not placed in its standard form and is slightly rotated, but this does not affect that it is a rectangle, and it still has all the properties of a rectangle.
The perimeter of a rectangle is the sum of all its sides, that is, to find the perimeter of the rectangle we will have to add the lengths of all the sides. We also know that in a rectangle the opposite sides are equal. Therefore, we can use the existing sides to complete the missing lengths.
4.8+4.8+12+12 = 33.6 cm
Answer
33.6 cm
Examples and exercises with solutions for the perimeter of a trapezoid
Exercise #1
Look at the rectangle below.
Side AB is 2 cm long and side BC has a length of 7 cm.
What is the perimeter of the rectangle?
Video Solution
Step-by-Step Solution
Since in a rectangle every pair of opposite sides are equal to each other, we can claim that:
AB=CD=2
AD=BC=7
Now we can add all the sides together and find the perimeter:
2+7+2+7=4+14=18
Answer
18 cm
Exercise #2
Look at the rectangle below.
Side AB is 4.8 cm long and side AD has a length of 12 cm.
What is the perimeter of the rectangle?
Video Solution
Step-by-Step Solution
In the drawing, we have a rectangle, although it is not placed in its standard form and is slightly rotated, but this does not affect that it is a rectangle, and it still has all the properties of a rectangle.
The perimeter of a rectangle is the sum of all its sides, that is, to find the perimeter of the rectangle we will have to add the lengths of all the sides. We also know that in a rectangle the opposite sides are equal. Therefore, we can use the existing sides to complete the missing lengths.
4.8+4.8+12+12 = 33.6 cm
Answer
33.6 cm
Examples and exercises with solutions for the perimeter of the triangle
Exercise #1
Look at the rectangle below.
Side AB is 2 cm long and side BC has a length of 7 cm.
What is the perimeter of the rectangle?
Video Solution
Step-by-Step Solution
Since in a rectangle every pair of opposite sides are equal to each other, we can claim that:
AB=CD=2
AD=BC=7
Now we can add all the sides together and find the perimeter:
2+7+2+7=4+14=18
Answer
18 cm
Exercise #2
Look at the rectangle below.
Side AB is 4.8 cm long and side AD has a length of 12 cm.
What is the perimeter of the rectangle?
Video Solution
Step-by-Step Solution
In the drawing, we have a rectangle, although it is not placed in its standard form and is slightly rotated, but this does not affect that it is a rectangle, and it still has all the properties of a rectangle.
The perimeter of a rectangle is the sum of all its sides, that is, to find the perimeter of the rectangle we will have to add the lengths of all the sides. We also know that in a rectangle the opposite sides are equal. Therefore, we can use the existing sides to complete the missing lengths.
4.8+4.8+12+12 = 33.6 cm
Answer
33.6 cm
Examples and exercises with solutions for the perimeter of the rectangle
Exercise #1
Look at the rectangle below.
Side AB is 2 cm long and side BC has a length of 7 cm.
What is the perimeter of the rectangle?
Video Solution
Step-by-Step Solution
Since in a rectangle every pair of opposite sides are equal to each other, we can claim that:
AB=CD=2
AD=BC=7
Now we can add all the sides together and find the perimeter:
2+7+2+7=4+14=18
Answer
18 cm
Exercise #2
Look at the rectangle below.
Side AB is 4.8 cm long and side AD has a length of 12 cm.
What is the perimeter of the rectangle?
Video Solution
Step-by-Step Solution
In the drawing, we have a rectangle, although it is not placed in its standard form and is slightly rotated, but this does not affect that it is a rectangle, and it still has all the properties of a rectangle.
The perimeter of a rectangle is the sum of all its sides, that is, to find the perimeter of the rectangle we will have to add the lengths of all the sides. We also know that in a rectangle the opposite sides are equal. Therefore, we can use the existing sides to complete the missing lengths.
4.8+4.8+12+12 = 33.6 cm
Answer
33.6 cm
Do you know what the answer is?
Question 1
Look at the rectangle below.
Side AB is 4.8 cm long and side AD has a length of 12 cm.
