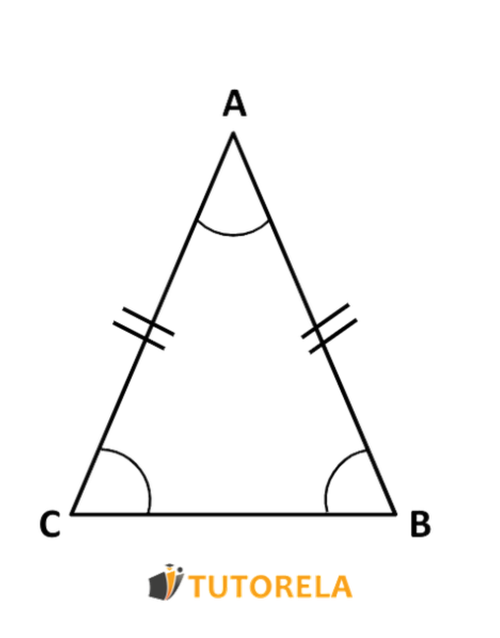
The isosceles triangle is a type of triangle that has two sides (legs) of equal length.
A consequence of having two sides of equal length implies that also the two angles opposite these sides measure the same.
Key Parts:
Legs: The two equal sides
Base: The third side (different length)
Vertex angle: The angle between the two legs
Base angles: The two equal angles adjacent to the base
This fundamental property—that equal sides create equal opposite angles—makes isosceles triangles essential building blocks in geometry and forms the basis for the Isosceles Triangle Theorem.
In a right triangle, the side opposite the right angle is called....?
Incorrect
Correct Answer:
Hypotenuse
Practice more now
In an isosceles triangle the two equal sides are called legs and the third is called the base and in most exercises acts as the base.
The angle that lies between the two equal sides is called the angle at the vertex (or apex angle).
The two angles adjacent to the base are called base angles and measure the same.
Furthermore, the base angles that measure the same cannot be obtuse (more than 90°) or right angles (equal to 90°), because their measures would add up to at least 180°, therefore, they have to be acute (less than 90°).
The above causes the isosceles triangle to be further classified as obtuse, right or acute, depending on how the vertex angle is.
The Isosceles Triangle Theorem: In any isosceles triangle, the base angles are equal. Conversely, if two angles in a triangle are equal, then the triangle is isosceles.
Next, we will see some examples of isosceles triangles:
Isosceles triangle
Examples of isosceles triangles
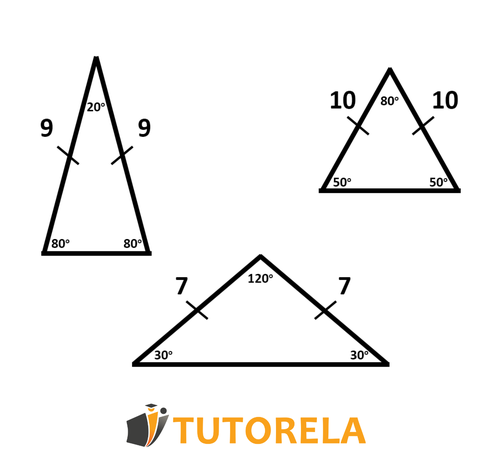
We will demonstrate the characteristics of isosceles triangles by means of an exercise.
Given the isosceles triangle △KLM as shown in the figure.
Example Question
Use the data shown in the illustration to calculate the angles L and M.
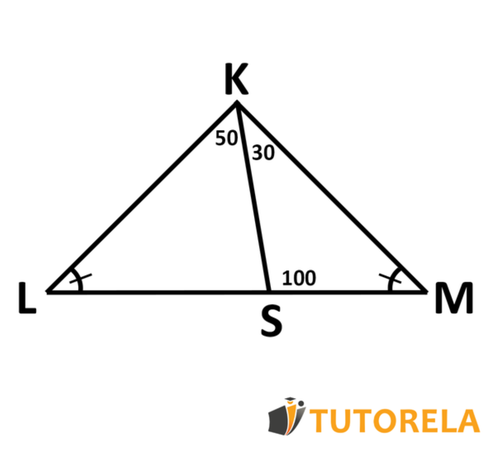
We will start with the triangle △KMS. We already know two angles, so we can calculate the third angle M (The sum of the interior angles of a triangle is 180° degrees). Thus, the angle M measures 50° degrees (since 50°=180°−100°−30°).
Since we know that the triangle △KLM is isosceles we understand that its base angles L and M are equal.
ThereforeL=M=50°
Join Over 30,000 Students Excelling in Math!
Endless Practice, Expert Guidance - Elevate Your Math Skills Today
Test your knowledge
Question 1
In an isosceles triangle, what are each of the two equal sides called ?
Incorrect
Correct Answer:
Legs
Question 2
In a right triangle, the two sides that form a right angle are called...?
Incorrect
Correct Answer:
Legs
Question 3
Is the triangle in the drawing an acute-angled triangle?
Incorrect
Correct Answer:
Yes
Questions on the subject
What is an isosceles triangle?
It is a triangle that has two sides of equal length.
What is an acute isosceles triangle?
It is an isosceles triangle whose angle at the vertex measures less than90°.
What is a right isosceles triangle?
It is an isosceles triangle whose angle at the vertex measures exactly 90°.
If you are interested in learning more about other triangle topics, you can enter one of the following articles:
On theTutorela blogyou will find a variety of articles about mathematics.
Ejemplos y ejercicios con soluciones de triángulo isósceles
Exercise #1
Is the triangle in the drawing an acute-angled triangle?
Video Solution
Step-by-Step Solution
An acute-angled triangle is defined as a triangle where all three interior angles are less than 90∘.
In examining the visual depiction of the triangle provided in the problem, we need to see if it appears to satisfy this property. The assessment relies on observing the triangle's structure shown in the drawing and noting any geometric indications suggesting angle types.
Given the information from the drawing, if all angles seem to satisfy the condition of being less than 90∘, then by definition, the triangle is an acute-angled triangle.
Conclusively, the answer to whether the triangle is acute-angled based on provided visual assessment and inherent assumptions in its illustration is: Yes.
Answer
Yes
Exercise #2
In an isosceles triangle, the angle between ? and ? is the "base angle".
Step-by-Step Solution
An isosceles triangle is one that has at least two sides of equal length. The angles opposite these two sides are known as the "base angles."
The side that is not equal to the other two is referred to as the "base" of the triangle. Thus, the "base angles" are the angles between each of the sides that are equal in length and the base.
Therefore, when we specify the angle in terms of its location or position, it is the angle between a "side" and the "base." This leads to the conclusion that the angle between the side and the base is the "base angle."
Therefore, the correct choice is Side, base.
Answer
Side, base.
Exercise #3
What kind of triangle is given in the drawing?
Video Solution
Step-by-Step Solution
As all the angles of a triangle are less than 90° and the sum of the angles of a triangle equals 180°:
70+70+40=180
The triangle is isosceles.
Answer
Isosceles triangle
Exercise #4
Given the values of the sides of a triangle, is it a triangle with different sides?
Video Solution
Step-by-Step Solution
As is known, a scalene triangle is a triangle in which each side has a different length.
According to the given information, this is indeed a triangle where each side has a different length.
Answer
Yes
Exercise #5
Which kind of triangle is given in the drawing?
Video Solution
Step-by-Step Solution
As we know that sides AB, BC, and CA are all equal to 6,
All are equal to each other and, therefore, the triangle is equilateral.
Answer
Equilateral triangle
Do you know what the answer is?
Question 1
Is the triangle in the drawing an acute-angled triangle?
Incorrect
Correct Answer:
Yes
Question 2
Is the triangle in the drawing an acute-angled triangle?
Incorrect
Correct Answer:
Yes
Question 3
Given the values of the sides of a triangle, is it a triangle with different sides?
