Arcs in a Circle

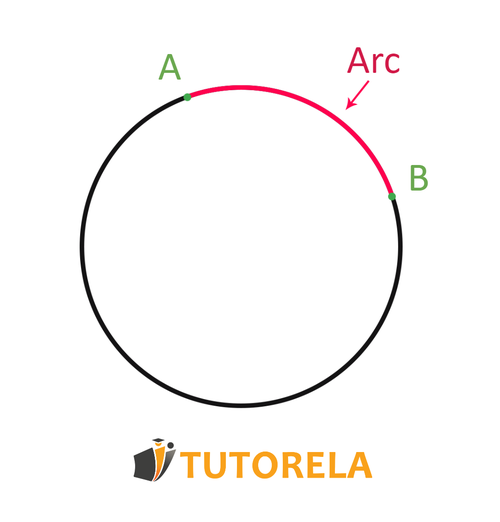
An arc is a portion of the circumference of a circle, the part that is between $2$ points on the circle.
The arc is part of the circumference of the circle and does not pass inside the circle.
Arcs are categorized as either major (larger than half the circle) or minor (smaller than half the circle).

More relevant components of the circle:

Radius: The distance from the center of the circle to any point on the circumference.
Diameter: A straight line passing through the center that connects two points on the circumference, equal to twice the radius.
Arc: A portion of the circumference.
Chord: A line segment connecting two points on the circle.
Tangent: A line that touches the circle at exactly one point.

Arc Length - Advanced

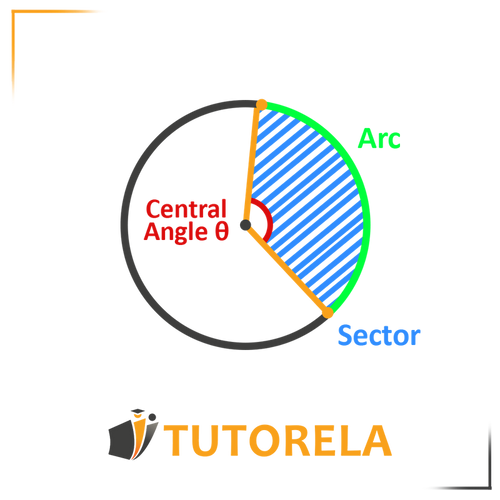
The central angle formed by two radii connecting the center to the arc determines its size. The distance along the arc can be calculated using the formula

$\text{Length} = \frac{\theta}{360} \times 2\pi r$

$\theta$ is the central angle in degrees.

Sector: The area bounded by two radii and the arc, resembling a slice of pie.

Detailed explanation

Start practice

Test yourself on the parts of a circle!

In which of the circles is the point marked in the circle and not on the circumference?

Practice more now

Arcs in a Circle

We are here to explain to you what an arc in a circle is in the easiest and most logical way.
First, let's remember what the shape of an arc is...
When you look up at the sky and see a rainbow, it looks like this, right?

How about a hair tie? It looks quite similar as well:

Now that we remember the shape of the arc, it will be easier for us to remember what an arc in a circle is.

What is an arc in a circle?

An arc in a circle is the part between $2$ points on the circle.
Pay attention: the arc is on the circle and not inside it. It is part of the circumference of the circle and closely resembles the rainbows we see in everyday life.

Let's show it in the figure:

In front of us is a circle.
If we take $2$ points on top of the circle, for example, $A$ and $B$ ,
the part of the circle between these two points will be an arc.
Pay attention that we do not draw a line between the points inside the circle (a chord)
but rather we paint the top part of the circle as part of its circumference.

Note:
The arc can be of any length and even if it does not remind us of the arc we see in everyday life, it will still be an arc in a circle.
While it is on the circle between $2$ points as part of the circumference, the circle is called an arc.
We will see examples where the arc in the circle does not look like an arc shape:

If you are interested in this article, you might also be interested in the following articles:

In the Tutorela blog, you will find a variety of articles about mathematics.

Examples and exercises with solutions of arcs in a circle

Exercise #1

A point whose distance from the center of the circle is _______ than the radius, is outside the circle.

Step-by-Step Solution

Let's remember that the circle is actually the inner part of the circumference, meaning the enclosed area within the frame of the circumference.

Therefore, a point whose distance is greater than the center of the circle will necessarily be outside the circle.

Answer

greater

Exercise #2

Where does a point need to be so that its distance from the center of the circle is the shortest?

Step-by-Step Solution

Let's remember that the circle is actually the inner part of the circumference, meaning the enclosed area within the frame of the circumference.

Therefore, a point whose distance is less than the radius from the center of the circle will necessarily be inside the circle.

Answer

Inside

Exercise #3

In which of the circles is the segment drawn the radius?

Video Solution

Step-by-Step Solution

Let's remember that a radius is a line segment connecting the center of the circle to a point that lies on the circle itself.

In drawing A, the line doesn't touch any point on the circle itself.

In drawing B, the line doesn't pass through the center of the circle.

We can see that in drawing C, the line that extends from the center of the circle is indeed connected to a point on the circle itself.

Answer

Exercise #4

Which diagram shows the radius of a circle?

Step-by-Step Solution

Let's remember that a radius is a line segment connecting the center of a circle to any point on the circle itself.

In drawing C we can see that the line coming from the center of the circle indeed connects to a point on the circle itself, while in the other drawings the lines don't touch any point on the circle.

Therefore, C is the correct drawing.