What do the diagonals in an isosceles trapezoid always form?

Two pairs of congruent triangles

A pair of isosceles triangles and a pair of congruent triangles

A pair of similar triangles and a pair of obtuse triangles

Isosceles Trapezoid

The isosceles trapezoid is, in fact, a trapezoid (that is, a four-sided polygon with two of them - the bases - being parallel), with two of its sides being equivalent and with its base angles of equal magnitude.

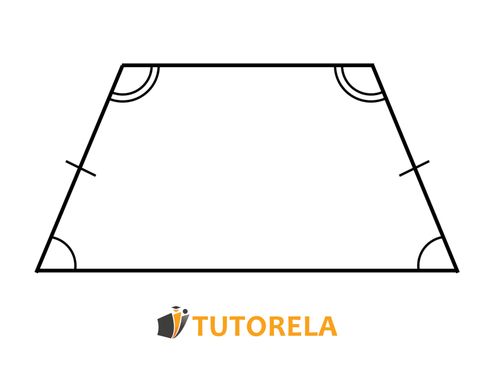
In the trapezoid, as is known, there are two bases and, each base has two base angles adjacent on both sides. In other words, in the isosceles trapezoid, there are two sets of equal base angles, as can be seen in the following illustration:

Isosceles Trapezoid

Detailed explanation

Start practice

Test yourself on isosceles trapezoids!

Below is an isosceles trapezoid

If $$ ∢D=50° $$

Determine the value of $$ ∢B $$ ?

Practice more now

Definition of an isosceles trapezoid

The isosceles trapezoid is, in fact, a trapezoid (that is, a four-sided polygon with two of them - the bases - being parallel), with two of its sides being equivalent and with its base angles of equal magnitude.

In the trapezoid, as is known, there are two bases and, each base has two adjacent base angles on both sides. In other words, in the isosceles trapezoid, there are two sets of equal base angles, as can be seen in the following illustration:

Isosceles Trapezoid

Isosceles Trapezoid Properties

The properties detailed here are the unique characteristics of isosceles trapezoids among all other types of trapezoids. The following illustration describes the theorems in the best way:

Properties of the Isosceles Trapezoid

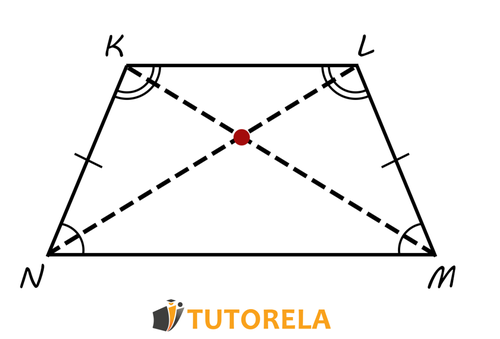
The sides that are not parallel are congruent, that is, they have the same measure. That is, it is fulfilled: $NK=LM$
In the isosceles trapezoid, there are two sets of equal angles for the larger base and for the smaller base.

That is, angles $L$ and $K$ are equivalent, just like angles $M$ and $N$ are also.

The two diagonals of the isosceles trapezoid are equal. That is, it is fulfilled: $KM=LN$
Any isosceles trapezoid can be inscribed in a circle

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Given: $$ ∢A=120° $$

The isosceles trapezoid

Find a: $$ ∢C $$

Question 2

Given: $$ ∢C=2x $$

$$ ∢A=120° $$

isosceles trapezoid.

Find x.

Question 3

True OR False:

In all isosceles trapezoids the base Angles are equal.

Demonstration of the Isosceles Trapezoid

To demonstrate that a trapezoid is isosceles, we must make use of the properties specified earlier, in fact, these are reciprocal theorems. It is sufficient to demonstrate just one property.

That is, if we prove that:

The two sides that are not parallel are congruent

The angles at the base of the trapezoid are congruent

The diagonals of the trapezoid are congruent

then, said trapezoid is an isosceles trapezoid.

The diagonals of an isosceles trapezoid

The following properties refer to the diagonals of the isosceles trapezoid. To highlight these properties in the best way, we will use this illustration:

Diagonals of the Isosceles Trapezoid

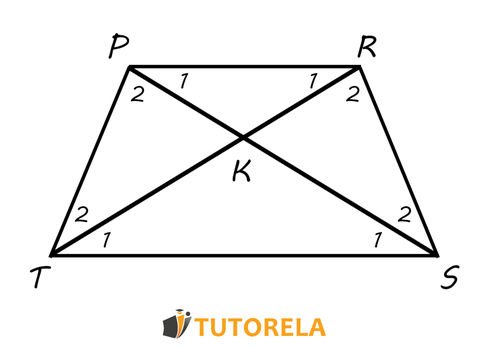
The two diagonals are equal. That is, it holds that: $PS=RT$
The triangles $PTS$ and $RST$ are congruent according to the side - side - side congruence theorem
The triangles $TPR$ and $SRP$ are congruent according to the side - side - side congruence theorem
The triangles $PKR$ and $TKS$ are isosceles triangles with all that this implies
The angles $P1$ , $R1$ , $S1$ , and $T1$ are equivalent

Do you know what the answer is?

Question 1

Do isosceles trapezoids have two pairs of parallel sides?

Question 2

Look at the polygon in the diagram.

What type of shape is it?

Question 3

In an isosceles trapezoid ABCD

$$ ∢B=3x $$

$$ ∢D=x $$

Calculate the size of angle $$ ∢B $$ .

Calculation of the Area of an Isosceles Trapezoid

The calculation of the area of an isosceles trapezoid is done exactly in the same way as the area of any other trapezoid is calculated.

That is, the lengths of the two bases are added, the total sum is multiplied by the height, and then, it is divided by $2$ .

We will use this illustration to explain the steps of the calculation:

Finding the area of an Isosceles Trapezoid

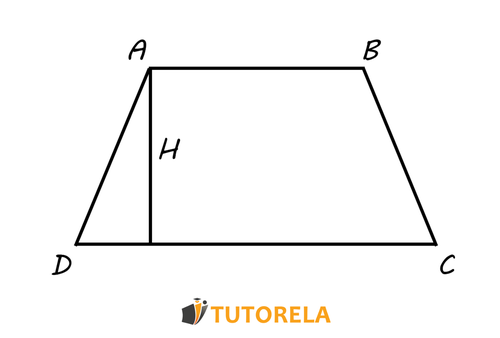
The formula to calculate the area of the isosceles trapezoid (not exclusively) is:

$A=\frac{ ( AB+ DC) \times H}{2}$

Examples and exercises with isosceles trapezoids

Exercise No 1

Given the isosceles trapezoid described in the following scheme.

It is known that the sum of three angles is $240º$ degrees.

According to the data, we must calculate all the angles of this isosceles trapezoid.

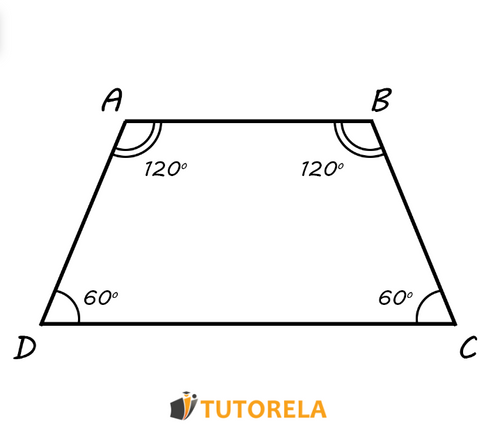
Solution:

If the sum of the three angles of the given trapezoid is $240º$ and the total sum of the angles of a trapezoid (as with any quadrilateral) is $360º$ , we can deduce that the fourth angle measures $120º$ degrees.

It is one of the adjacent angles to the smaller base, let's assume angle $A$ . Since it is an isosceles trapezoid, the angles at the base are congruent, therefore, angle $B$ also measures $120º$ .

Remember that it is a trapezoid and that the bases $AB$ and $DC$ are parallel, that is, angles $A$ and $D$ (just like $B$ and $C$ ) are collateral angles and, therefore, complement each other and together measure $180º$ degrees. Therefore, it will give us that angles $C$ and $D$ measure $60º$ degrees.

Answer:

The angles of the trapezoid are $120º, 120º, 60º, 60º$

Check your understanding

Question 1

In an isosceles trapezoid, will the sum of the opposite angles always be 180°?

Question 2

Are the diagonals of an isosceles trapezoid equal and do they intersect each other?

Question 3

Do the diagonals of the trapezoid necessarily bisect each other?

Exercise No 2

Given the isosceles trapezoid described in the following scheme.

It is known that the sum of two of its sides is $120º$ .

According to the data, we must calculate all the angles of this isosceles trapezoid.

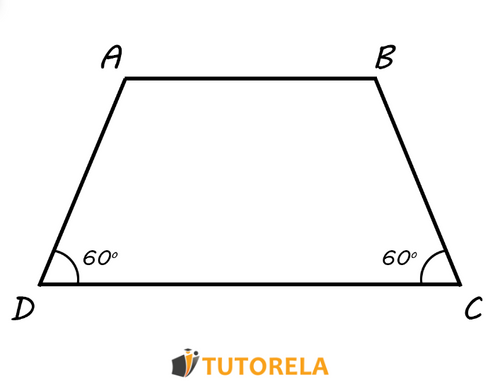
Solution:

Let's go back to the rules related to the base and remember that it is a trapezoid and that the bases $AB$ and $DC$ are parallel, that is, the angles $A$ and $D$ (as well as $B$ and $C$ ) are collateral angles and, therefore, complement each other and together measure $180º$ degrees. Given that the amplitude we have is $120º$ degrees, we can deduce that these are not adjacent angles on the same side (i.e., unilateral), but angles that share the same base.

Being an isosceles trapezoid, the base angles are congruent, therefore, each of them measures $60º$ degrees.

The complementary angle (to reach $180º$ degrees) of each of these angles measures $120º$ degrees.

Answer:

The angles of the trapezoid are $120º, 120º, 60º, 60º$

Examples and exercises with solutions of isosceles trapezoid

Exercise #1

Given: $∢C=2x$

$∢A=120°$

isosceles trapezoid.

Find x.

Video Solution

Step-by-Step Solution

Given that the trapezoid is isosceles and the angles on both sides are equal, it can be argued that:

$∢C=∢D$

$∢A=∢B$

We know that the sum of the angles of a quadrilateral is 360 degrees.

Therefore we can create the formula:

$∢A+∢B+∢C+∢D=360$

We replace according to the existing data:

$120+120+2x+2x=360$

$240+4x=360$

$4x=360-240$

$4x=120$

We divide the two sections by 4:

$\frac{4x}{4}=\frac{120}{4}$

$x=30$

Answer

30°

Exercise #2

Below is an isosceles trapezoid

If $∢D=50°$

Determine the value of $∢B$ ?

Video Solution

Step-by-Step Solution

Let's recall that in an isosceles trapezoid, the sum of the two angles on each of the trapezoid's legs equals 180 degrees.

In other words:

$A+C=180$

$B+D=180$

Since angle D is known to us, we can calculate:

$180-50=B$

$130=B$

Answer

130°

Exercise #3

Do isosceles trapezoids have two pairs of parallel sides?

Step-by-Step Solution

To solve this problem, we'll follow these steps:

Step 1: Define the geometric properties of a trapezoid.
Step 2: Define the geometric properties of an isosceles trapezoid.
Step 3: Conclude whether an isosceles trapezoid has two pairs of parallel sides based on these definitions.

Now, let's work through each step:
Step 1: A trapezoid is defined as a quadrilateral with at least one pair of parallel sides.
Step 2: An isosceles trapezoid is a special type of trapezoid where the non-parallel sides (legs) are of equal length. Its defining feature is having exactly one pair of parallel sides, which is the same characteristic as a general trapezoid.
Step 3: Since the definition of a trapezoid inherently allows for only one pair of parallel sides, an isosceles trapezoid, as a type of trapezoid, cannot have two pairs of parallel sides. A quadrilateral with two pairs of parallel sides is typically designated as a parallelogram, not a trapezoid.

Therefore, the solution to the problem is that isosceles trapezoids do not have two pairs of parallel sides. No.

Answer

Exercise #4

True OR False:

In all isosceles trapezoids the base Angles are equal.

Video Solution

Step-by-Step Solution

True: in every isosceles trapezoid the base angles are equal to each other.

Answer

True

Exercise #5

In an isosceles trapezoid, will the sum of the opposite angles always be 180°?

Step-by-Step Solution

Let's closely examine the properties of an isosceles trapezoid to determine the relationship between its opposite angles.

An isosceles trapezoid is a type of trapezoid where the non-parallel sides (legs) are of equal length. It also implies that the angles adjacent to each leg are equal, due to the symmetry of the trapezoid. However, the most crucial aspect for this problem involves understanding the sum of angles in a trapezoid and their specific relationships.

Consider an isosceles trapezoid, $ABCD$ , with base $AB$ parallel to base $CD$ , and legs $AD$ and $BC$ being equal.

The key property in any trapezoid is that each pair of angles on the same side of one of the non-parallel sides ( $AD$ or $BC$ ) are supplementary. That is, angles $\angle DAB$ and $\angle ABC$ together sum to $180^\circ$ since they are co-interior angles formed by a transversal cutting the parallel lines $AB$ and $CD$ .
Similarly, angles $\angle BCD$ and $\angle CDA$ also sum to $180^\circ$ .

In addition, the total sum of the interior angles of any quadrilateral (and thus any trapezoid) is $360^\circ$ . Therefore, opposite angles $\angle DAB$ and $\angle BCD$ (first set) sum to $180^\circ$ , and similarly, opposite angles $\angle ABC$ and $\angle CDA$ (second set) also sum to $180^\circ$ . Therefore, the sum of the opposite angles in an isosceles trapezoid is always $180^\circ$ .

Thus, through application of the properties of parallel lines and angle sums, we find that the sum of opposite angles in an isosceles trapezoid is indeed always $180^\circ$ .

The correct conclusion of this problem is that the statement is True.

The sum of the opposite angles in an isosceles trapezoid is always $180^\circ$ .

Answer

True

Do you think you will be able to solve it?

Question 1

The perimeter of the trapezoid equals 22 cm.

AB = 7 cm

AC = 3 cm

BD = 3 cm

What is the length of side CD?

Question 2

Given: $$ ∢A=y+20 $$

$$ ∢D=50 $$

The trapeze is isosceles.

Find a $$ ∢A $$

Question 3

Below is an isosceles trapezoid.

$$ ∢B=2y+20 $$

$$ ∢D=60 $$

Find $$ ∢B $$ .

Start practice

Isosceles Trapezoid

Isosceles Trapezoid

Test yourself on isosceles trapezoids!

Definition of an isosceles trapezoid

Isosceles Trapezoid Properties

Demonstration of the Isosceles Trapezoid

The diagonals of an isosceles trapezoid

Calculation of the Area of an Isosceles Trapezoid

Examples and exercises with isosceles trapezoids

Exercise No 1

Exercise No 2

Examples and exercises with solutions of isosceles trapezoid

Exercise #1

Video Solution

Step-by-Step Solution

Answer

Exercise #2

Video Solution

Step-by-Step Solution

Answer

Exercise #3

Step-by-Step Solution

Answer

Exercise #4

Video Solution

Step-by-Step Solution

Answer

Exercise #5

Step-by-Step Solution

Answer

More Questions

Isosceles Trapezoids