Circuit Components

Diagram of a circle illustrating geometric components: center 'M,' chord AB, secant line AF, arc AC, and radii MD and ME. The image highlights the relationships between chords, secants, and arcs in circle geometry

$AB$ chord
$AC$ arc
$DME$ central angle is $2$ times larger than inscribed angle $DFE$ – both intercepting the same arc

Detailed explanation

Start practice

Test yourself on the parts of a circle!

Is it correct to say:

'the circumference of a circle'?

Practice more now

Circle Components

Chord

A chord in a circle is a straight line that passes through the circle and connects any 2 points located on the circle.
Remember: The chord passes through the circle and not on it.

Is a radius a chord?
Absolutely not. A radius connects a point outside of the circle to the center point of the circle. A chord, on the other hand, connects 2 points on the circle.
Is a diameter a chord?
Yes! A diameter connects 2 points on the circle. In fact, the longest chord in a circle is called a diameter!

Click here to learn more about a chord in a circle

arc

Illustration of a circle highlighting an arc AB. The arc is a curved section of the circle's circumference between points A and B. This geometric diagram is useful for understanding circle properties, arcs, and segment relationships

An arc in a circle is part of the circle's circumference and does not pass through the circle.
An arc is essentially the part between any 2 points on the circle and its shape is like a rainbow.
The arc can be small, large, or even almost the entire circumference of the circle.
Note - it does not pass through the circle like a chord.
Let's see an example of arcs in a circle:

Illustration of three different circle arcs. Each diagram highlights a distinct arc section of a circle's circumference in orange. These geometric diagrams help in understanding circle properties, arcs, and segment relationships in mathematics.

Click here to learn more about arcs in a circle

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Where does a point need to be so that its distance from the center of the circle is the shortest?

Question 2

A point whose distance from the center of the circle is _______ than the radius, is outside the circle.

Question 3

Identify which diagram shows the radius of a circle:

Central angle in a circle

A central angle in a circle is an angle whose vertex is at the center of the circle and its rays are radii of the circle.
In other words, if we draw 2 radii - 2 straight lines, we create an angle called a central angle.

Mathematical diagram of a circle with two radii forming a sector. The center of the circle is labeled 'M,' and the highlighted orange lines represent the radii connecting the center to two points on the circumference. This illustration helps in understanding circle sectors and radius properties in geometry.

Click here to read more about central angles in a circle

Equal central angles

We can determine that central angles are equal when:
Case 1:
If the angles are subtended by equal arcs, we can determine that the central angles are equal.
Similarly, we can determine that if the central angles are equal, their corresponding arcs are also equal to each other.
or
Case 2:
If the chords opposite to the angles are equal, we can determine that the central angles are equal.

Similarly, we can determine that if the central angles are equal, their corresponding chords are also equal to each other.

The relationship between the central angle and the inscribed angle in a circle:
In a circle, the central angle is twice the size of the inscribed angle that intercepts the same arc.
Alternatively, the inscribed angle is equal to half of the central angle that intercepts the same arc.

Geometric diagram of a circle labeled with center 'M' and points D, E, and F on the circumference. The orange lines represent radii and chords, illustrating different segments within the circle. This diagram is useful for understanding circle properties, such as radius, chord, and central angles in geometry.

Angle $DME$ is 2 times larger than angle $DFE$

A perpendicular from the center of the circle to a chord

A perpendicular to a chord is a straight line that extends from the center of the circle to the chord.
The perpendicular bisects the chord into two equal parts and creates a right angle between the perpendicular and the chord.
Additionally, the perpendicular bisects the central angle that subtends the chord into two equal parts and bisects the arc opposite the chord into two equal parts.
Similarly, we can say that if a straight line extends from the center of the circle and bisects a chord, it will be perpendicular to that chord.

Mathematical diagram of a circle labeled with center 'M' and a triangle inscribed within it. The triangle is isosceles, with equal radii from the center to the circumference, a perpendicular bisector, and right angle markings. This diagram illustrates key circle properties such as radii, chords, perpendicular bisectors, and central symmetry in geometry.

Click here to learn more about perpendicular from circle center to chord

The distance of a chord from the center of the circle

The distance of a chord from the center of the circle is the length of the perpendicular line connecting the center of the circle to the chord.
• Chords that are equal in length are at equal distances from the center of the circle.
• If the distance of a chord from the center of the circle is smaller than the distance of another chord from the center of the circle, then we can determine that the chord with the smaller distance is longer than the other chord.

Mathematical diagram of a circle with two perpendicular diameters intersecting at the center. Right angles are marked where the diameters bisect each other and the chords. This geometric representation illustrates symmetry and perpendicularity in circles.

You can learn more about this in this link

Do you know what the answer is?

Question 1

Identify which diagram shows the radius of a circle:

Question 2

In which of the circles is the point marked inside of the circle and not on the circumference?

Question 3

Calculate the length of the arc marked in red given that the circumference is 12.

inscribed angle

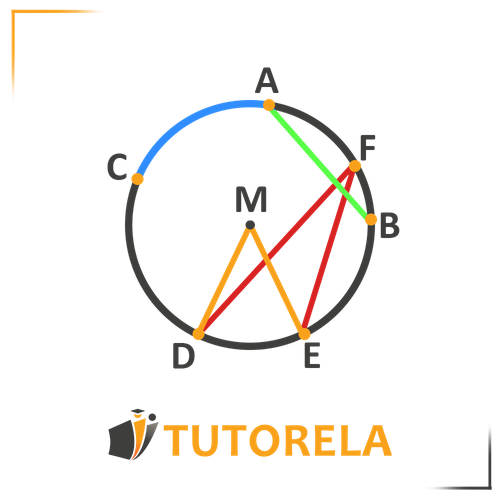
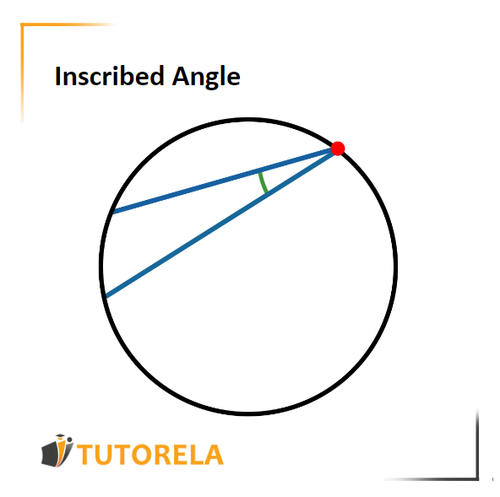
An inscribed angle in a circle is an angle whose vertex is on the circumference of the circle - meaning on the circle and not inside it, and its rays are chords of the circle.

Equal inscribed angles

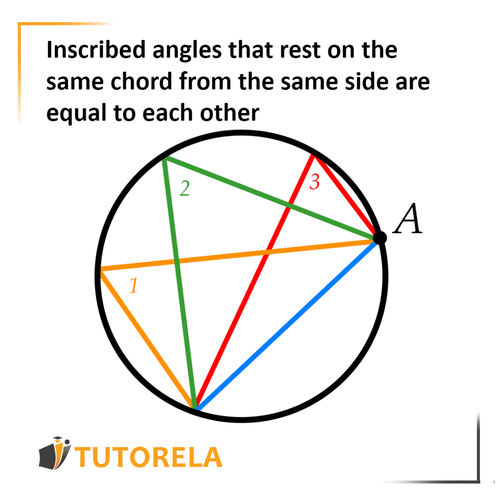
Inscribed angles that are based on the same chord from the same side are equal inscribed angles.
and
Equal inscribed angles are opposite to equal chords and equal arcs.

A3 - Inscribed angles that lean on the same chord from the same side are equal to each other

tangent

A tangent to a circle is a line that touches the circle at one point and is perpendicular to the radius at the point of tangency.

Mathematical diagram of a circle with a chord and its perpendicular bisector. The chord is marked with endpoints on the circumference, while the bisector extends from the center, forming a right angle. This geometric representation highlights the perpendicular bisector theorem and symmetry in circles.

• The angle between a tangent and any chord equals the inscribed angle subtending the same chord
from the other side.
• Two tangents to a circle drawn from the same point are equal in length.
• The line segment connecting the center of the circle to the point from which two tangents are drawn
bisects the angle between the tangents.
• If from a point outside the circle, a tangent and a secant are drawn, then the product of the entire
secant and its external part equals the square of the tangent.
• In a triangle circumscribing a circle, the three angle bisectors of the triangle intersect at a single
point at the center of the circle.

Click here to read more about tangent to a circle

Check your understanding

Question 1

Calculate the length of the arc marked in red given that the circumference is 12.

Question 2

Calculate the length of the arc marked in red given that the circumference is 6.

Question 3

Calculate the length of the arc marked in red given that the circumference is 36.

Examples with solutions for The Parts of a Circle

Exercise #1

A point whose distance from the center of the circle is _______ than the radius, is outside the circle.

Step-by-Step Solution

Let's remember that the circle is actually the inner part of the circumference, meaning the enclosed area within the frame of the circumference.

Therefore, a point whose distance is greater than the center of the circle will necessarily be outside the circle.

Answer

greater

Exercise #2

Where does a point need to be so that its distance from the center of the circle is the shortest?

Step-by-Step Solution

Let's remember that the circle is actually the inner part of the circumference, meaning the enclosed area within the frame of the circumference.

Therefore, a point whose distance is less than the radius from the center of the circle will necessarily be inside the circle.

Answer

Inside

Exercise #3

In which of the circles is the point marked inside of the circle and not on the circumference?

Video Solution

Step-by-Step Solution

Let's remember that the circular line draws the shape of the circle, and the inner part is called a disk.

Therefore, in diagram B, the point is located in the inner part, meaning inside the disk.

Answer

Exercise #4

Identify which diagram shows the radius of a circle:

Step-by-Step Solution

Remember that a radius is a line segment connecting the center of a circle to any point on the circle itself.

In drawing C we can see that the line coming from the center of the circle indeed connects to a point on the circle itself, while in the other drawings the lines don't touch any point on the circle.

Therefore, C is the correct drawing.

Answer

Exercise #5

Identify which diagram shows the radius of a circle:

Video Solution

Step-by-Step Solution

Remember that a radius is a line segment connecting the center of the circle to a point that lies on the circle itself.

In drawing A, the line doesn't touch any point on the circle itself.

In drawing B, the line doesn't pass through the center of the circle.

We can see that in drawing C, the line that extends from the center of the circle is indeed connected to a point on the circle itself.

Answer

Start practice

Circuit Components