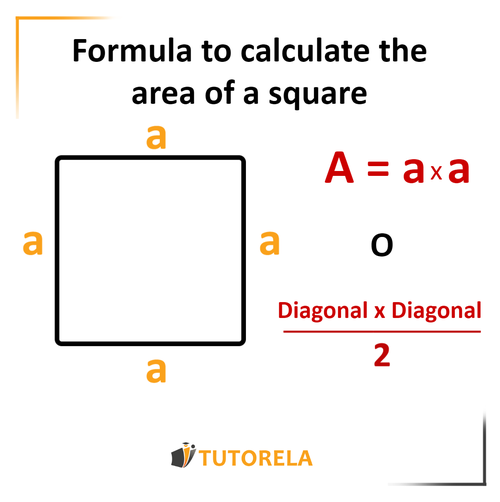
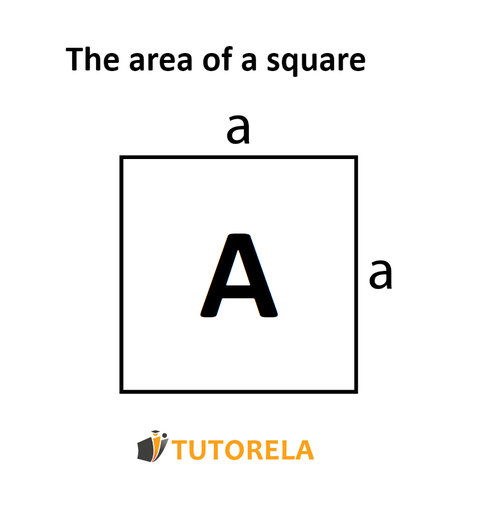
The area of a square represents the amount of space inside its four equal sides. It is calculated using the formula:
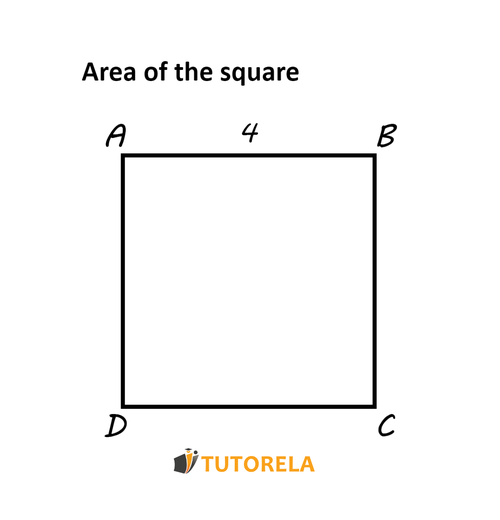
Let's take this square as an example:
The area will be: or
where : represents the area of the square
and –> is the length of the edge (or side) of the square
Another way to calculate the square's area is by the diagonals:
Look at the square below:
What is the area of the square equivalent to?
Calculating the area of a square is one of the simplest there is and works in a similar way to the area of a rectangle.
To calculate the area of a square we must multiply one side by itself.
This is because it is as if we multiplied the length by the height, just as is done with the rectangle.
Since all sides of the square are equal we will multiply side by side, or rather, we will calculate side squared.
The formula will look like this:
or
where -> represents the area of the square
and –> is the length of the edge (or side) of the square
Given:
square
What is the area of the square?
Solution:
The side of the square measures , we place it in the area calculation formula and we will obtain :
The area of the square is .
If you are interested in this article, you might also be interested in the following articles:
Multiplication of the Sum of Two Elements by the Difference Between Them
The Formula for the Difference of Squares
The Formulas Relating to Two Expressions to the Power of 3
In the blog of Tutorela you will find a variety of articles about mathematics.
Look at the square below:
What is the area of the square?
Remember that the area of the square is equal to the side of the square raised to the second power
The formula for the area of the square is:
We calculate the area of the square:
Look at the square below:
What is the area of the square equivalent to?
The area of a square is equal to the square of its side length.
In other words:
Since in the diagram we are given one side of the square, and in a square all sides are equal to each other, we will solve for the area of the square as follows:
Look at the square below:
What is the area of the square?
The area of the square is equal to the side of the square raised to the second power.
That is:
Since the diagram provides us with one side of the square, and in a square all sides are equal, we will solve the area of the square as follows:
Look at the square below:
What is the area of the square?
The area of the square is equal to the side of the square raised to the second power.
That is:
Since the drawing gives us one side of the square, and in a square all sides are equal, we will solve the area of the square as follows:
Look at the square below:
What is the area of the square?
The area of the square is equal to the side of the square raised to the second power.
That is:
Since the drawing gives us one side of the square, and in a square all sides are equal, we will solve the area of the square as follows:
Look at the square below:
What is its area?
Look at the square below:
What is the area of the square?
Look at the square below:
What is the area of the square?
