Corresponding exterior angles

Angles in Parallel Lines - Examples, Exercises and Solutions
🏆Practice angles in parallel lines
5 Questions
Parallel and Perpendicular Lines
Angles in Parallel Lines
Practice
Add a new subject

Alternate exterior angles

Alternate exterior angles are alternate angles located in the external part outside the parallel lines. Furthermore they are not on the same side of the transversal nor are they on the same level (floor) relative to the line.

Diagram illustrating corresponding exterior angles in geometry with two highlighted red angles on a polygon structure, used to explain the concept of angle relationships in educational content."

Start practice

Test yourself on angles in parallel lines!

Does the diagram show an adjacent angle?

Practice more now

Alternate exterior angles

To begin with let's discuss the general characteristics of alternate angles:

Alternate angles between parallel lines are equal.
They are called alternate angles due to the fact that they:
• Are not on the same side of the transversal line
• Are not on the same "level" relative to the line

Here is an example of alternate angles:

Diagram illustrating corresponding exterior angles in geometry with two highlighted red angles on a polygon structure, used to explain the concept of angle relationships in educational content."


Given that the two marked angles are not on the same level nor are they on the same side, they can be considered as alternate angles.
In order to understand what exterior alternate angles are, you must observe that:
There is the exterior part - outside the two parallel lines
As well as an interior part - between the two parallel lines.
Let's examine the illustration:

Diagram explaining corresponding exterior and interior angles with labeled sections: the exterior part in orange, the interior part in blue, and highlighted angles for geometry demonstration, designed for teaching angle relationships.


In the illustration, we observe that the two alternate angles located outside the two parallel lines are exterior alternate angles.

Let's look at another example of alternate exterior angles:

Diagram illustrating corresponding exterior angles in geometry with two highlighted red angles on a polygon structure, used to explain the concept of angle relationships in educational content."

In this illustration both alternate angles are once again located in the external part and therefore they can be considered to be exterior alternate angles.

Bonus tip!
Alternate angles located in the inner part between two parallel lines are called alternate interior angles.

Now let's practice!
Here are two parallel lines and a line intersecting them.
a. Determine whether the angles shown are alternate angles.
b. Determine whether they are also alternate exterior angles.

Diagram illustrating corresponding exterior angles in geometry with two highlighted red angles on a polygon structure, used to explain the concept of angle relationships in educational content."

Solution:
a. Yes, the angles in the figure are alternate angles. They are not on the same side of the transversal and not on the same level.
b. Yes, the alternate angles in the figure are exterior since they are located in the external part outside the two parallel lines.

Another exercise:
Two parallel lines and a transversal line intersecting them are shown.
Determine if the angles shown are alternate angles
b. Determine if they are alternate exterior angles.

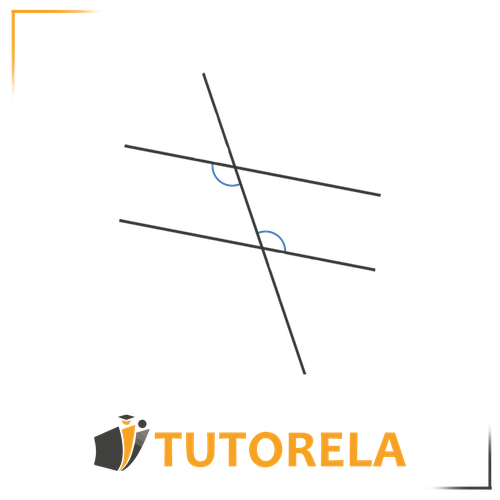
Diagram showing corresponding interior angles in geometry with marked arcs in blue and connecting lines, featuring a quadrilateral structure and labeled by Tutorela.


Solution:
a. Yes, the angles in the figure are alternate angles. They are not on the same level and not on the same side of the transversal.
b. No. The angles are located in the internal part between the two parallel lines, therefore they are alternate angles but not exterior.

Additional exercise:
Here are two parallel lines and a line that intersects them.
Find the size of angle WW
and determine whether angle W and angle QQ are alternate exterior angles.
Given that: Q=120Q=120

Diagram demonstrating corresponding exterior angles in geometry, marked as 'w' and 'q' in blue, within a quadrilateral structure for educational purposes.

Solution:
According to the given information, we can determine that angle WW and angle QQ are alternate angles. They are located between two parallel lines, each on a different side of the transversal and not on the same level.
Alternate angles are equal to each other, therefore if Q=120Q=120 we can conclude that angle W=120W=120

Additionally, we can determine that the two angles are alternate exterior angles due to the fact that they are both located on the outer side of the lines.

Additional Exercise:
Determine in which of the drawings there are equal alternate exterior angles and explain why.
In all drawings, the two lines are parallel to each other.

1.

Diagram illustrating corresponding exterior angles in geometry with two highlighted red angles on a polygon structure, used to explain the concept of angle relationships in educational content."


2.

Diagram showing corresponding interior angles in geometry with marked arcs in blue and connecting lines, featuring a quadrilateral structure and labeled by Tutorela.

Solution:
In the first drawing, the two angles are alternate exterior angles since they are located in the external part of the lines
and in the second drawing, the two angles are alternate interior angles since they are located in the internal part of the lines.

More exercises:
Determine true or false:

Between parallel lines-
a. Alternate exterior angles are not equal to each other.
b. Alternate exterior angles are located in the external part outside both parallel lines.
c. Alternate angles sum to 180180.

Solution:
a. Incorrect – alternate exterior angles are equal to each other (and alternate interior angles are equal to each other).
b. Correct – this is why they are called alternate exterior angles.
c. Incorrect – alternate angles are not supplementary to 180180 but are equal to each other (regardless of whether they are exterior or interior).

Join Over 30,000 Students Excelling in Math!
Endless Practice, Expert Guidance - Elevate Your Math Skills Today
Test your knowledge
Question 1

Does the diagram show an adjacent angle?

Question 2

Does the diagram show an adjacent angle?

Question 3

Does the diagram show an adjacent angle?

Examples with solutions for Angles in Parallel Lines

Exercise #1

Does the diagram show an adjacent angle?

Video Solution

Step-by-Step Solution

To determine if the diagram shows adjacent angles, we need to analyze the geometric arrangement shown:

  • Step 1: Identify the common vertex.

    In the diagram, both the vertical line and the diagonal line intersect at a point. This intersection point serves as the common vertex for the angles in question, as they radiate outward from this shared point.

  • Step 2: Identify the common side.

    Adjacent angles must share a common side or arm. In the diagram, the vertical line acts as one common side for both angles, with one angle extending upwards and the other horizontally from the vertex.

  • Step 3: Ensure no overlap of interiors.

    It is equally essential to ensure that these two angles do not overlap. Each angle branches from the vertex in a different direction, maintaining distinct interiors.

By confirming the presence of a common vertex and a common side without overlap of the angle interiors, the angles satisfy the definition of being adjacent.

Therefore, the diagram does indeed show adjacent angles.

Consequently, the correct answer is Yes.

Answer

Yes

Exercise #2

Does the diagram show an adjacent angle?

Video Solution

Step-by-Step Solution

To determine whether the diagram shows adjacent angles, we need to confirm the presence of two properties:
1. Two angles must share a common vertex.
2. These angles must have a common arm and should not overlap.

Based on the given representation, the provided diagram consists solely of a single line. There are no visible intersecting lines or vertices from which angles can originate. Without intersection, there cannot be distinct angles, and thereby no adjacent angles can be identified.

Therefore, the diagram lacks the necessary properties to demonstrate adjacent angles. Hence, the correct choice is No.

Answer

No

Exercise #3

Does the diagram show an adjacent angle?

Video Solution

Step-by-Step Solution

To solve this problem, we'll follow these steps:

  • Step 1: Inspect the given diagram for angles.
  • Step 2: Determine if any angles share a common vertex and a common side.
  • Step 3: Verify that the angles do not overlap.

Now, let's work through each step:

Step 1: Inspecting the diagram, we notice several intersecting lines.

Step 2: To check for adjacent angles, we look for pairs of angles that share both a common vertex and a common side. An adjacent angle must be formed by such pairs, ensuring they do not overlap.

Step 3: Based on our definition, after closely examining the diagram, no pair of angles in the diagram seems to satisfy the definition of adjacent angles. The intersecting lines form angles that don't share a common arm with any other angle at the same vertex in the manner required for adjacency.

Therefore, the solution to the problem is No, the diagram does not show an adjacent angle.

Answer

No

Exercise #4

If two adjacent angles are not right angles, then one of them is obtuse and the other is acute.

Video Solution

Step-by-Step Solution

To solve the problem, let’s consider the nature of adjacent angles:

  • Step 1: Adjacent angles are two angles that share a common side and vertex. If two adjacent angles form a straight line, their measures sum up to 180∘180^\circ.
  • Step 2: According to the problem, neither angle is a right angle, meaning neither is 90∘90^\circ.
  • Step 3: Given this constraint, analyze the possibilities:
    • If one angle is acute (less than 90∘90^\circ), then the other must be more than 90∘90^\circ to make the total 180∘180^\circ. Therefore, the other angle is obtuse.
    • If one angle is obtuse (greater than 90∘90^\circ), then the other must be less than 90∘90^\circ to make the total 180∘180^\circ. Thus, the other angle is acute.

Since both scenarios involve one angle being acute and the other obtuse, we verify that the statement is correct.

Therefore, the statement is true.

Answer

True

Exercise #5

It is possible for two adjacent angles to be right angles.

Video Solution

Step-by-Step Solution

To determine if it is possible for two adjacent angles to be right angles, we start by considering the definition of adjacent angles. Adjacent angles share a common side and a common vertex. We must think about this scenario in terms of the angles lying on a straight line or a flat plane.

A right angle is exactly 90∘90^\circ. Hence, if we have two right angles that are adjacent, their measures would be:

  • First angle: 90∘90^\circ
  • Second angle: 90∘90^\circ

When these two angles are adjacent, as defined in the problem, their sum is:

90∘+90∘=180∘ 90^\circ + 90^\circ = 180^\circ

Angles that are adjacent along a straight line add up exactly to 180∘180^\circ. Therefore, it is indeed possible for two adjacent angles to be both 90∘90^\circ. This configuration simply means that these two angles lie along a straight line, dividing it into two right angles.

Hence, the statement is True.

Answer

True

Start practice

More Questions

Related Subjects
👉  Click here  to practice