Triangle

In this article, we will briefly learn everything necessary about triangles and also practice with some exercises!
Let's get started!

Detailed explanation

Start practice

Test yourself on triangle!

Complete the sentence:

To find the area of a right triangle, one must multiply ________________ by each other and divide by 2.

Practice more now

The Parts of a Triangle - What Is It Made Of?

Line: It is the union of a sequence of points, which are located in a linear way, that is, there are no curves between them.
Segment: It is a portion of a line, which is joined between two points.
Height: The height of a triangle is the measure or length from a vertex to the highest point of the triangle, it is usually denoted with the letter h.
Median: the median is the segment that extends from a given vertex to the midpoint of the opposite side to that vertex.
Bisector: the bisector is a ray that extends from a given vertex, dividing it into two equal angles.
Perpendicular bisector: the perpendicular bisector is the line that exactly halves its sides and can be drawn perpendicular to those sides.
Middle segment: In the case of triangles, the middle segment is that line that we can draw by locating the midpoint of two sides, this line will measure half of the third side.
Opposite side: an opposite side is one that is located in front of a given vertex.

The triangle is a figure composed of $3$ sides and the sum of all its angles always equals $180$ degrees.
There are several types of triangles:

Equilateral triangle - All sides (or edges) are equal, all angles are equal, and all heights are also the median and the bisector.
Isosceles triangle - It has two equal sides, two equal base angles, and the median is also the height and the bisector.
Right triangle - It has an angle of $90$ degrees formed by two legs. The side opposite the right angle is called the hypotenuse.
Scalene triangle - All sides of the triangle are different.

Click here for a more in-depth explanation about the types of triangles.

Triangle Angles

In any triangle, regardless of the type of triangle it is, the sum of all its angles equals $180 º$ .
In the equilateral triangle -> each angle is $60 º$ degrees.
In the isosceles triangle -> the two base angles are equal and the third completes the $180 º$ .
In the right triangle -> only one angle is $90 º$ and the other two complete the $180 º$ .

Another note:
In the special triangle of 90 º , 45 º , 45 º -> only one angle is $90 º$ and the other two are $45 º$ each, this creates a triangle that is both isosceles and right at the same time.

Exercise:
Given the following angles:
angle $A=80 º$
angle $B=50 º$
angle $C=50 º$

Click here for a more in-depth explanation about the angles of triangles.

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Calculate the area of the right triangle below:

Question 2

Calculate the area of the triangle using the data in the figure below.

Question 3

Calculate the area of the triangle below, if possible.

Area of the Triangle

Here we will present the general formula for calculating the area of triangles:

A3 - the general formula for calculating the area of triangles

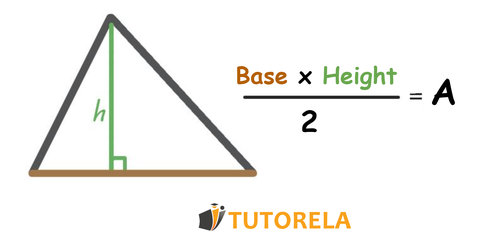
This formula is used to calculate the area of isosceles, equilateral, and scalene triangles.
Right triangle

length of the first leg $\times$ length of the second leg
\frac{length~of~the~first~leg~\times ~length~of~the~second~leg

Click here for a more in-depth explanation about the area of the triangle.

Perimeter of the triangle

The perimeter of the triangle is equal to the sum of the lengths of all sides.

In an equilateral triangle – all sides are equal, therefore, the perimeter of the triangle will be $3\cdot side$
In an isosceles triangle - there are two equal sides and it is convenient to remember this when we want to deduce the perimeter

Click here for a more in-depth explanation about the perimeter of the triangle.

Do you know what the answer is?

Question 1

Calculate the area of the triangle below, if possible.

Question 2

Find the perimeter of the triangle ABC

Question 3

Find the perimeter of the triangle ABC

Triangle Congruence

Triangles are considered congruent if all their angles and all their sides are equal respectively.
To prove that two triangles are congruent you must demonstrate one of the following congruence theorems:

ASA – angle, side, angle
If both triangles have 2 equal angles and the length of the side between them is also equal, the triangles are congruent.

SAS – side, angle, side
If both triangles have 2 equal sides and the adjacent angle is also equal, the triangles are congruent.

SSS - Side, side, side
If the lengths of all 3 sides are equal respectively in both triangles, the triangles are congruent.

SSA - Side, side, angle
If the 2 sides are equal in both triangles and so is the angle opposite the larger side, the triangles are congruent.

Click here for a more in-depth explanation on triangle congruence.

Similarity of Triangles

Similar triangles do not need to have identical areas as is the case with congruent triangles, it is enough that they have the same proportions.
To prove that two triangles are similar you must demonstrate one of the following similarity theorems:

AA – Angle, Angle
If two angles of one triangle are equal to two angles of the other, the triangles are similar.

SSS - Side, Side, Side
If in one triangle the three sides are proportional to the three sides of the other, the triangles are similar.

Click here for a more in-depth explanation on the similarity of triangles.

Examples and exercises with solutions of triangles

Exercise #1

Find the perimeter of the triangle ABC

Video Solution

Step-by-Step Solution

To find the perimeter of triangle $\triangle ABC$ , we need to sum the lengths of its sides:

Side $AB = 3$
Side $BC = 4$
Side $CA = 5$

Using the formula for the perimeter of a triangle:

$\text{Perimeter} = AB + BC + CA$

Substitute the known values:

$\text{Perimeter} = 3 + 4 + 5$

$\text{Perimeter} = 12$

Thus, the perimeter of triangle $\triangle ABC$ is $\mathbf{12}$ .

From the multiple-choice options provided, the correct choice is option 1: 12.

Answer

Exercise #2

Find the perimeter of the triangle ABC

Video Solution

Step-by-Step Solution

To solve this problem, we'll follow these steps:

Step 1: Identify the given information.
Step 2: Apply the perimeter formula for a triangle.
Step 3: Perform the addition to find the perimeter.

Now, let's work through each step:

Step 1: We have the lengths of the sides of $\triangle ABC$ as follows:
$AB = 7$ , $BC = 14$ , and $CA = 8$ .

Step 2: We'll use the formula for the perimeter of a triangle, which is the sum of its side lengths:
$P = AB + BC + CA$ .

Step 3: Plugging in the values, we calculate:
$P = 7 + 14 + 8 = 29$ .

Therefore, the perimeter of $\triangle ABC$ is $\textbf{29}$ .

Answer

Exercise #3

Complete the sentence:

To find the area of a right triangle, one must multiply ________________ by each other and divide by 2.

Step-by-Step Solution

To solve this problem, begin by identifying the elements involved in calculating the area of a right triangle. In a right triangle, the two sides that form the right angle are known as the legs. These legs act as the base and height of the triangle.

The formula for the area of a triangle is given by:

A = \frac{1}{2} \times \text{base} \times \text{height}

In the case of a right triangle, the base and height are the two legs. Therefore, the process of finding the area involves multiplying the lengths of the two legs together and then dividing the product by 2.

Based on this analysis, the correct way to complete the sentence in the problem is:

To find the area of a right triangle, one must multiply the two legs by each other and divide by 2.

Answer

the two legs

Exercise #4

Calculate the area of the following triangle:

Video Solution

Step-by-Step Solution

The formula for calculating the area of a triangle is:

(the side * the height from the side down to the base) /2

That is:

$\frac{BC\times AE}{2}$

We insert the existing data as shown below:

$\frac{4\times5}{2}=\frac{20}{2}=10$

Answer

Exercise #5

Calculate the area of the triangle using the data in the figure below.

Video Solution

Step-by-Step Solution

To solve the problem of finding the area of triangle $\triangle ABC$ , we follow these steps:

Step 1: Identify the given measurements.
Step 2: Use the appropriate formula for the area of a triangle.
Step 3: Calculate the area using these measurements.

Let's go through each step in detail:
Step 1: From the figure, the base $AB = 10$ and height $AC = 2$ .
Step 2: The formula for the area of a triangle is: $\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$ .
Step 3: Substituting the known values into the formula, we get:

$\text{Area} = \frac{1}{2} \times 10 \times 2 = \frac{1}{2} \times 20 = 10$

Therefore, the area of triangle $\triangle ABC$ is 10.

Answer

Check your understanding

Question 1

Calculate the area of the following triangle:

Question 2

Calculate the area of the following triangle:

Question 3

Calculate the area of the triangle below, if possible.

Start practice

Triangle

Triangle

Test yourself on triangle!

The Parts of a Triangle - What Is It Made Of?

Triangle Angles

Area of the Triangle

Perimeter of the triangle

Triangle Congruence

Similarity of Triangles

Examples and exercises with solutions of triangles

Exercise #1

Video Solution

Step-by-Step Solution

Answer

Exercise #2

Video Solution

Step-by-Step Solution

Answer

Exercise #3

Step-by-Step Solution

Answer

Exercise #4

Video Solution

Step-by-Step Solution

Answer

Exercise #5

Video Solution

Step-by-Step Solution

Answer

More Questions

Triangle

Area of a Triangle

Perimeter of a Triangle