Area of a right-angled trapezoid

Before we begin, let's recall some properties of a right-angled trapezoid:
Properties of a right-angled trapezoid

• In a right-angled trapezoid, there are 2 angles equal to 90 degrees each.
• The leg connecting the 2 right angles is also the height of the trapezoid!
• In a right-angled trapezoid - the total sum of angles is 360 degrees, where 2 angles are equal to 90 degrees each and the other 2 angles sum up to 180.

Let's observe this in an illustration:

In order to calculate the area of a right-angled trapezoid, we will use the following formula:

The area of a right-angled trapezoid equals the sum of the bases multiplied by the height divided by 2.

Exercise:
Given the following trapezoid, calculate its area.

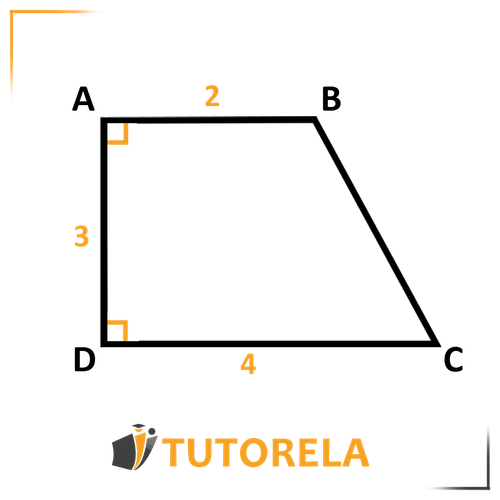
Given:
angle $A = 90$
angle $D = 90$

$AB= 2$
$DC= 4$
$AD= 3$

Solution:
We are told that there are 2 right angles in the trapezoid, therefore we are able to determine that it is a right-angled trapezoid.
In order to calculate the area of the trapezoid, we need to add the two bases, multiply by the height and divide the result by 2.
We know that in a right-angled trapezoid, the height is also the side connecting the two right angles, meaning $AD = 3$.
Therefore:
We'll add the given bases $AD + CD$ and multiply by the height $AD$ and divide this by $2$. We obtain the following:
$\frac{(2+4) \cdot3} {2} =$

$\frac{18}{2}=9$
The area of the trapezoid is $9$ cm².

Additional Exercise

Here is the following right-angled trapezoid:

Given that:
Angle $A = 90$
Angle $B = 100$
Angle $C = 80$
$AD= 2$
$AB = 5$
$DC = AB+1$

What is the area of the trapezoid?

Solution:
To begin with, we need to look at all the given information and identify what type of trapezoid we are dealing with.
We are given one angle equal to $90$ degrees and $2$ other angles that together equal $180$ degrees.
We know that the sum of angles in a trapezoid equals $360$ degrees, therefore angle $D$ must equal $90$ degrees.
We can observe that in this trapezoid there are $2$ angles that equal $90$ degrees each, therefore it is a right-angled trapezoid.
To calculate the area of a right-angled trapezoid, we need to know the lengths of the bases and the height.
The height in a right-angled trapezoid is also the side connecting the two right angles - meaning side $AD= 2$
The two bases are: $AB$ and $DC$
According to the given information: $AB = 5$ and $DC= AB+1$
Therefore
$DC = 6$
Let's calculate using the right-angled trapezoid area formula and we should obtain the following:

$\frac{(6+5) \cdot2} {2} = 11$

The area of the trapezoid is $11$ cm².

Additional Exercise:

Given that:
The area of the trapezoid is $25$ cm²
Angle $D= 20$
Angle $A = 90$
Angle $B = 90$
We know that the sum of bases is $25$.
Determine the length of side $AB$ and the size of side $C$.

Solution:
We can confirm straightaway that this is a right-angled trapezoid given that it has $2$ angles equal to $90$ .
We are given the area of the trapezoid and we need to find the height - $AB$
If we recall the formula for finding the area of a right-angled trapezoid and substitute the sum of the bases and the given area of the trapezoid, we obtain the following:

$\frac{(25) \cdot AB} {2} =25$
We can clearly see that $AB$ must be $2$ in order to obtain a true statement, therefore the height of the trapezoid $AB$ equals $2$.

The size of side $C$ needs to be completed to $180$.
It is known that angle $D$ equals $20$ and therefore $C$ equals $160$.