Types of Trapezoids

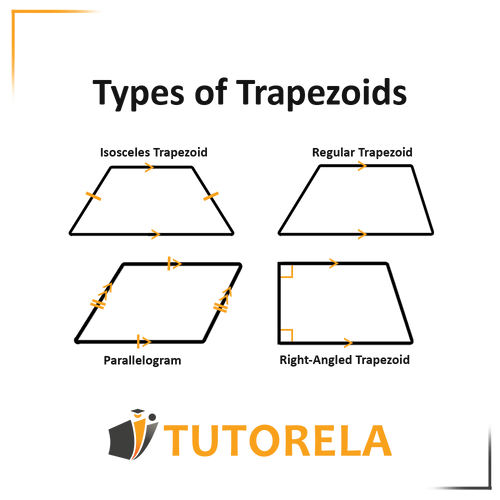
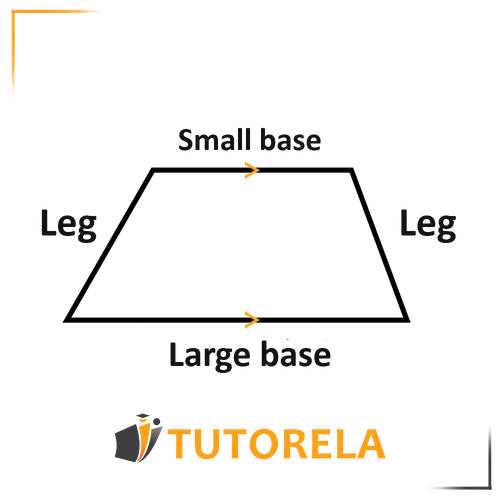
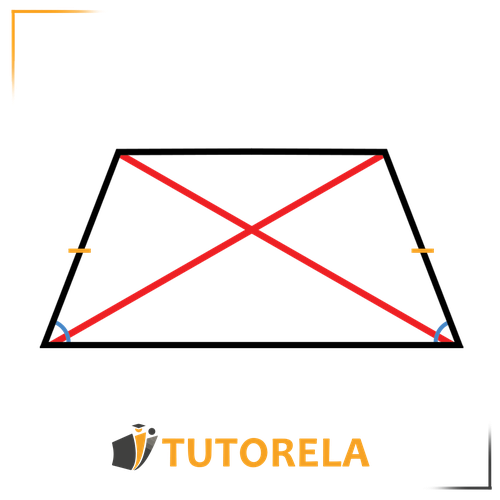
A Standard Trapezoid is a quadrilateral that:

• Exactly one pair of parallel sides, called the bases
• Two non-parallel sides, called the legs or lateral sides
• The perpendicular distance between the bases is called the height

• One pair of parallel sides
• Adjacent angles on the same leg are supplementary (sum to 180°)
• All interior angles sum to 360°
• A diagonal creates equal alternate interior angles between parallel lines
• The midsegment (connecting midpoints of the legs) is parallel to the bases and equals half their sum

$Area =\frac{Sum~of~the~bases \cdot Height~to~the~base}{2}$

A scalene trapezoid is a trapezoid where:

• All four sides have different lengths
• No angles are congruent
• No sides are congruent except for the defining parallel bases
• Has no lines of symmetry

Properties:

• Exactly one pair of parallel sides
• All sides have different lengths
• All angles have different measures
• Diagonals are unequal in length
• Most general form of trapezoid

An isosceles trapezoid is a trapezoid where the two non-parallel sides (legs) are equal in length.

The properties of an isosceles trapezoid include all the properties of a standard trapezoid plus the following properties:

• Exactly one pair of parallel sides (bases)
• Non-parallel sides (legs) are congruent
• Base angles are congruent (angles on same base are equal)
• Opposite angles are supplementary (sum to 180°)
• Diagonals are congruent
• Has exactly one line of symmetry (perpendicular bisector of the parallel sides)
• Can be inscribed in a circle
• Diagonals divide each other in the same ratio

Let's see this in the diagram:

Click here to learn more about an isosceles trapezoid and even practice some exercises on the topic.

A right trapezoid is a trapezoid that has 2 right angles, each equal to 90 degrees.

The properties of a right trapezoid are:

• Exactly one pair of parallel sides
• Two consecutive right angles (90°)
• The leg connecting the right angles serves as the height
• The other two angles are supplementary (sum to 180°)
• One leg is perpendicular to both bases
• No lines of symmetry (unless it's also isosceles)

Let's see this in the illustration:

How do you calculate the area of a right-angled trapezoid?

Just like calculating the area of a standard trapezoid, according to the formula:

$Sum~of~the~bases \cdot height~to~the~base \over 2$

here, the height is the perpendicular leg!

1. General Trapezoid: Basic quadrilateral with one pair of parallel sides
2. Isosceles Trapezoid: Legs are equal, has line of symmetry
3. Scalene Trapezoid: All sides different lengths, no symmetry
4. Right Trapezoid: Has two right angles
5. Acute Trapezoid: All angles less than 90°
6. Obtuse Trapezoid: Has at least one obtuse angle

Practice:

Given the following trapezoid:

It is known that angles $A$ and $B$ are each equal to $90$ degrees.
It is also known that the leg on which angles $A$ and $B$ rest is equal to $5$ cm.

Additionally, the sum of the bases in the trapezoid is $15$ and angle $C$ is equal to $60$.

• Find the angle $D$.
• Calculate the area of the trapezoid.

Solution

We know it is a right-angled isosceles trapezoid based on the given information where both angle $A$ is $90$ degrees and angle $B$ is $90$ degrees.
Therefore, the sum of the other $2$ angles is $180$ degrees.
It is given that $C = 60$ degrees.
Therefore, $D = 120$ degrees
$180-60=120$
We substitute the data into the area formula for a right-angled trapezoid and get:
$\frac{15.5 * 5}{2}$