Area of an isosceles trapezoid

Properties of an isosceles trapezoid:

• In an isosceles trapezoid, the 2 legs are equal.
• In an isosceles trapezoid, the base angles are equal.
• In an isosceles trapezoid, the diagonals are equal.

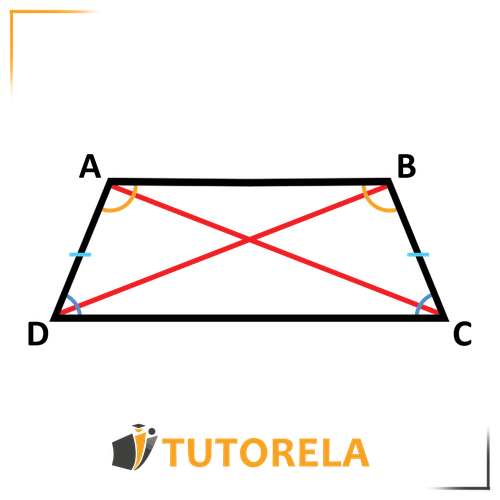
Important point - The midsegment of a trapezoid equals half the sum of the bases.
Reminder - A midsegment is a straight line that extends from the middle of one leg of a trapezoid to the middle of the other leg.

In order to calculate the area of an isosceles trapezoid, we need to multiply the height by the sum of the bases and divide by 2.
Therefore:

It often comes in handy to remember that mid-segment in a trapezoid equals half the sum of the bases.
Now what? Let's move on to practice.
Don't worry, we'll start with simple exercises and continue to more advanced ones.

Exercise:
Given an isosceles trapezoid

Given that:
$AB =4$
$DC=6$
$BE = 2$ and also height to trapezoid

What is the area of the trapezoid?

Solution:
In order to calculate the area of the trapezoid, we first need to add the bases, multiply by the height, and then divide by $2$.
According to the given data, the upper base $AB =4$ , and the lower base $DC= 6$
We get:
$\frac{(6+4) \cdot 2}{2} = 10$

The area of the trapezoid is $10$ cm².

Another exercise:
Here is an isosceles trapezoid

Given that:
$AB =3$
$DC=5$
$DE = 3$
Angle $BED = 90$
$EC=BE$

What is the area of the trapezoid?

Solution
We know that in order to calculate the area of a trapezoid, we need to know the sum of the two bases and the height.
The two bases are given to us and their sum is $8$.
Now all we need to do is to determine the height.
Let's note that angle $BED = 90$. This indicates that segment $BE$ is the height of the trapezoid.
We are also given that $EC=BE$, thus if we find $EC$ we will discover the height $BE$
We know that $DC=5$ and that $DE = 3$
Therefore $EC$ must equal $2$ because the whole is equal to the sum of its parts.
So the height equals $2$.
The area of the trapezoid is:
$\frac{8 \cdot 2} {2} = 8$
$8$ square cm.

Additional Exercise:
Here is a trapezoid.

Calculate the area of the trapezoid given that:
$BE=CE=AF=DF$
$FE=7$
$AG=3$
angle $AGD = 90$

Solution:
In order to calculate the area of the trapezoid, we need to determine what is the sum of the bases and what is the height.
We are given that angle $AGD = 90$ which means that $AG$ is the height of the trapezoid.
According to the given data $AG=3$.
We now need to understand what is the sum of the bases.
Note - we are given that: $BE=CE=AF=DF$
This means that the trapezoid is an isosceles trapezoid and segment $FE$ divides the legs exactly in the middle. Only in this way can a situation arise where all halves are equal.
Therefore, we can determine that $FE$ is a midsegment in the trapezoid - a line extending from the middle of one leg to the middle of the other leg.
We know that a midsegment in a trapezoid equals half the sum of the bases.
According to the given data $FE=7$ which means that the sum of the bases is $14$.

Now all that remains to do is to substitute into the trapezoid area formula and determine the area of the trapezoid:

$\frac{14 \cdot 3} {2} = 21$

The area of the trapezoid is $21$ cm².

Click here to read more about the midsegment in a trapezoid!

Another exercise:

Given an isosceles trapezoid.
Given that the area of the trapezoid is $14$ cm².
Find the height of the trapezoid $AG$
We know that $FE$ is the midsegment of the trapezoid and equals $5$.

Solution:
We know that in a trapezoid, the midsegment equals half the sum of the bases, so the sum of the bases is $10$.
Let's substitute the given data into the formula and we should obtain the following:
$\frac{10 \cdot AG}{2} = 20$
$40=10AG$
$AG=4$
The height of the trapezoid $AG$ is $4$.