From Parallelogram to Rhombus

How will you realize that the parallelogram in front of you is a rhombus?
We are here to teach you 3 criteria by which you can demonstrate, quickly and simply, that you have a rhombus in front of you.

First let's remember the definition of a rhombus.
The definition of a rhombus says the following: it is a parallelogram that has a pair of sides (or edges) adjacent that are equal.

If the parallelogram has a pair of equal adjacent sides, it is a rhombus.
You can use this theorem to show that it is a rhombus without having to prove it.
However, for you to understand the logic behind it, we will demonstrate this theorem below.

Data:

Parallelogram $ABCD$
$AB=BC$

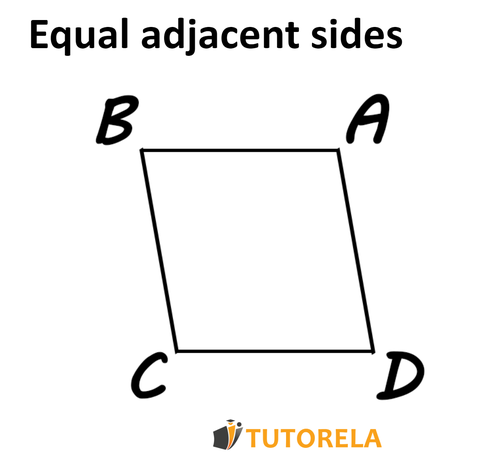
We have to prove that: $ABCD$ is a rhombus

Solution:
Since we have that $ABCD$ is a parallelogram, we deduce that:

$AB=DC$
$AD=BC$ because, in the parallelogram, each pair of opposite sides are also equivalent.

Let's observe our data $BC=AB$
Now, we can determine that all sides of the parallelogram are equivalent according to the transitive relation.
We obtain:
$AB=DC=BC=AD$

Indeed, $ABCD$  is a quadrilateral with all its sides equal, therefore, it is a rhombus.

If in the parallelogram the diagonals bisect each other forming angles of $90^o$ degrees, that is, they are perpendicular, it is a rhombus.

You can use this theorem to show that it is a rhombus without having to prove it.
However, for you to understand the logic behind it, we will demonstrate this theorem below.

Data:
Parallelogram $ABCD$
$AC⊥BD$

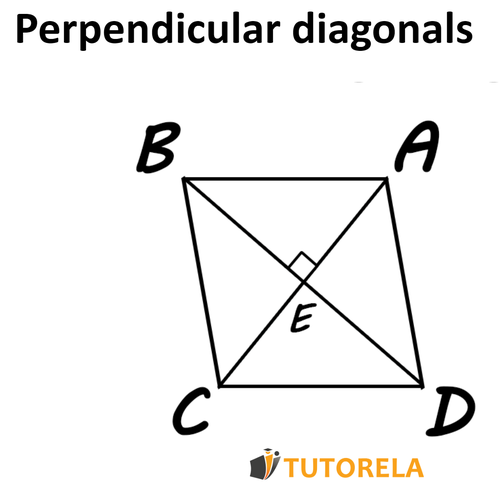
It must be demonstrated that: $ABCD$ is a rhombus

Solution:
Based on the first criterion, we already know that, it is enough for us to see that in the parallelogram there are two adjacent equivalent sides for us to know that it is a rhombus.
We can see that there is in this parallelogram a pair of adjacent equivalent sides if we use the congruence of triangles $ABE$ and $BEC$.
We will place them on top of each other:
Side $AE=AE$ common side, of the same length.
Angle $∢AEB=∢BEC$  These angles measure 90º since we know that the diagonals that create them are perpendicular.
Side $AE=CE$  in the parallelogram, the diagonals intersect

From this it follows that: $⊿ABE=⊿BEC$ according to SAS
And, consequently,
we will be able to determine that: $AB=BC$

According to the congruence, corresponding sides are equivalent.

We will notice that $AB$ and $BC$ are adjacent equivalent sides in the parallelogram and, therefore, we will be able to determine that $ABCD$ is a rhombus since a parallelogram with a pair of adjacent equivalent sides is a rhombus.

If in the parallelogram one of the diagonals is the bisector - it is a rhombus.

You can use this theorem to show that it is a rhombus without having to prove it.
However, for you to understand the logic behind it, we will prove this theorem below.

Data:
Parallelogram $ABCD$  
$∢c1=∢c2$

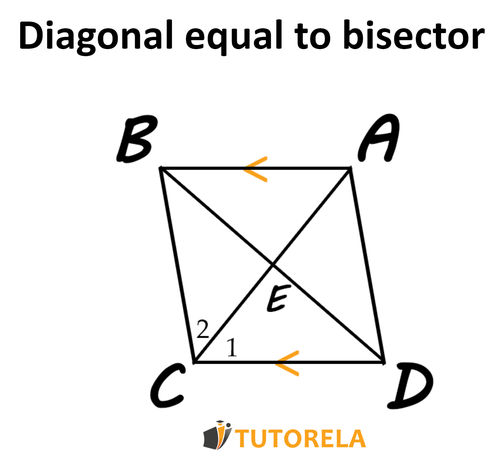
We have to prove that: $ABCD$ is a rhombus

Solution:
Let's remember, a parallelogram that has a pair of equal adjacent sides is a rhombus.
Let's start:
From the data we have we can deduce $AB∥DC$ since in a parallelogram, the opposite sides are also parallel.
Then: $∢BAC=∢C1$, alternate angles between parallel lines are equivalent.
According to the transitive relation, $∢BAC=∢C2$.
Now we can deduce that: $AB=BC$
In the triangle, opposite equivalent angles there are sides equal to each other.
Now we can determine that $ABCD$ is a rhombus.
We found in the parallelogram a pair of equal adjacent sides, therefore, it is a rhombus.

Suggestion:
To remember the three theorems that prove that a parallelogram is a rhombus, try to remember the three key terms: sides, diagonals, and angles.

Great!
Now you know all the criteria to prove that a parallelogram is a rhombus.