Decimal Fractions

Decimal Numbers

Meaning of the Decimal Number

The decimal number represents, through the decimal point (or comma in certain countries), a simple fraction or a number that is not whole.
The decimal point divides the number in the following way:

Detailed explanation

Start practice

Test yourself on decimal fractions - advanced!

Choose the correct writing form:

Practice more now

Reduction and Amplification of Decimal Numbers

Amplification of Decimal Numbers
We will add the digit $0$ to the end of the decimal number (to the right), and thus, the value of the decimal number will not change.
Reduction of Decimal Numbers
If the digit in the far-right position is $0$ , we will remove it and the value of the decimal number will not change.

Addition and Subtraction of Decimal Numbers

We will solve these operations vertically keeping in mind the following rules:
• We will take into account the rules of addition and subtraction of integers.
• Decimal points must always be positioned one below the other.
• We will write the numbers in an orderly manner - both to the right of the decimal point and to its left. (tenths below tenths, hundredths below hundredths, and so on)

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Determine whether the exercise is correctly written or not.

Question 2

Determine whether the exercise is correctly written or not.

Question 3

Determine whether the exercise is correctly written or not.

The position of the decimal point corresponds.

Comparison of Decimal Numbers

First step:
We will control the whole parts - the decimal number with the largest whole number will be the largest of them.
Second step:
In case the whole numbers are identical we will check the digits that appear after the point.
We will go digit by digit (starting with the tenths, then hundredths, and so on)
If they continue to be equal, we proceed with the comparison of the following ones.
If they are different, we can determine which number is the largest.

Conversion of Decimal Number to Fraction

Let's see how to read the fraction
If we use the word tenths, we will place $10$ in the denominator
If we use the word hundredths, we will place $100$ in the denominator
If we use the word thousandths, we will place $1000$ in the denominator.

We will place the number itself in the numerator.
*If the integer figure differs from $0$ , we will note it next to the simple fraction.

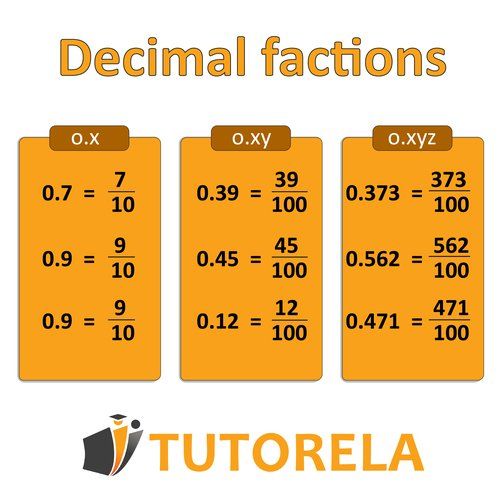
Chart illustrating the conversion of decimal numbers to fractions, categorized by one-digit, two-digit, and three-digit decimals, including examples like 0.7 = 7/10 and 0.562 = 562/100.

Do you know what the answer is?

Question 1

Determine whether the exercise is correctly written or not.

The position of the decimal point corresponds.

Question 2

Determine whether the exercise is correctly written or not.

True or false:

The positions of the decimal points correspond.

Question 3

Determine whether the exercise is correctly written or not.
The position of the decimal point corresponds.

Conversion from Decimal Number to Mixed Number

First, we will convert the decimal number to a fraction according to the rules.
Then, we will convert the simple fraction to a mixed number using the following method:
We will calculate how many whole times the numerator fits into the denominator - this will be the whole number.
What remains, we will write in the numerator, and the denominator will remain unchanged (does not change).

Multiplication and Division of Decimal Numbers by 10, 100, etc.

In multiplications: we will slide the decimal point to the right as many steps as the number has zeros.
In divisions: we will slide the decimal point to the left as many steps as the number has zeros.

Check your understanding

Question 1

Determine whether the exercise is correctly written or not.

The position of the decimal point corresponds.

Question 2

Determine whether the exercise is correctly written or not.

The position of the decimal point corresponds.

Question 3

Determine whether the exercise is written correctly in relation to the position of the decimal point:

Multiplication of Decimal Numbers

We will solve using the vertical multiplication method according to the following steps:
*We will write the numbers neatly one under the other, including the decimal points, one under the other, tenths under tenths, hundredths under hundredths, etc.
*We will solve the exercise, for now, we will not pay attention to the decimal point and will only act according to the rules of vertical multiplication.
*We will review each number in the exercise and count how many digits there are after the decimal point.
We will add up the total number of digits that are after the decimal point (taking into account both numbers) and that will be the number of digits that will be after the decimal point in the final answer.

Division of Decimal Numbers

We will proceed in the following order:
First step -> We will make the decimal point in the dividend (the number we want to divide) disappear, moving it to the right the necessary number of places until it is completely gone.
Second step -> In the divisor (the second number in the operation, that is, the number by which it is divided) we will move the decimal point to the right the same number of places that we moved in the first number (even if this number of steps is not enough to make it disappear)
Third step -> We will solve the "new" exercise (with the "new" numbers).

Do you think you will be able to solve it?

Question 1

Is the following written in the correct format?

Question 2

Is the following written in the correct format?

Question 3

Determine whether the exercise is written correctly:

Is the position of the decimal point correct in each number?

Repeating Decimal

A repeating decimal is a number with a fractional part that, after the decimal point, the digits repeat infinitely, in a periodic manner.
To learn how to convert a fraction to a repeating decimal, consult the complete article on this topic.

Decimal Measurements

To equalize decimal measures, we will proceed as follows:
We will identify the largest unit of measure between the two numbers, convert the number with the smaller unit of measure to the larger unit of measure, and compare both numbers that now have the same unit of measure.

Test your knowledge

Question 1

Is the following written in the correct format?

Question 2

Choose the correct format:

Question 3

Choose the correct writing form:

Density

Between any pair of numbers, there is an infinite number of other numbers.

Examples and exercises with solutions on decimal fractions

Exercise #1

Choose the correct writing form:

Video Solution

Step-by-Step Solution

To solve this problem, we'll follow these steps:

Step 1: Align the decimal numbers by their decimal points.
Step 2: Check if each digit is correctly aligned with its corresponding digit based on place value.
Step 3: Ensure the operation symbol is properly placed.

Now, let's work through each step:
Step 1: Start with the number 13.45 and align 3.21 directly below it such that the decimal points are vertically aligned. This ensures that the tenths, hundredths, and whole numbers are in the correct columns.
Step 2: Verify that: - The '1' in 13.45 is in the tens place, and the '3' in 3.21 is in the ones place, both aligned left of the decimal. - The '3' in 13.45 and '2' in 3.21 are aligned in the tenths column. - The '4' in 13.45 and '1' in 3.21 are in the hundredths column.
Step 3: Place the '+' sign outside and to the left, in line with the numbers, ensuring it is clearly indicating addition.

Therefore, the correct alignment for the addition of these decimal numbers is:

Answer

Exercise #2

Determine whether the exercise is correctly written or not.

Video Solution

Step-by-Step Solution

Note that the decimal points are not written one below the other. They do not correspond.

Therefore, the exercise is not written correctly.

Answer

Not true

Exercise #3

Determine whether the exercise is correctly written or not.

Video Solution

Step-by-Step Solution

Note that the decimal points are not written one below the other. They do not correspond.

Therefore, the exercise is not written correctly.

Answer

Not true

Exercise #4

Determine whether the exercise is correctly written or not.

The position of the decimal point corresponds.

Video Solution

Step-by-Step Solution

To determine if the addition problem is set up correctly, we need to analyze how the numbers are aligned.

The given numbers for addition are $312.54$ and $1203.22$ . When aligning these numbers for addition:

$\begin{array}{r} 312.54 \\ +1203.22 \\ \hline \end{array}$

We examine how the decimal points are positioned. For a correct setup, the decimal points should be aligned vertically. However, in the visual provided:

The decimal point in $312.54$ is positioned one place to the right compared to the decimal in $1203.22$ .
The alignment should have appeared as $\begin{aligned} &\phantom{00}312.54 \\ &+1203.22 \end{aligned}$ to be correct, but it does not.

Since the decimal points are not vertically aligned, the addition is set up incorrectly.

Therefore, the statement regarding the positioning of the decimal points is Not true.

Answer

Not true

Exercise #5

Determine whether the exercise is correctly written or not.

The position of the decimal point corresponds.

Video Solution

Step-by-Step Solution

To determine whether the exercise is set correctly, we need to align the decimal points of the two numbers involved in the subtraction operation:

1. The given numbers are 38.15 and 122.3.
2. We write them down vertically, aligning by the decimal points:

$\begin{array}{c} \hphantom{0}38.15 \\ - \hphantom{0}122.3 \\ \end{array}$

3. Notice that the number 38.15 has two decimal places (hundredths), while 122.3 only has one decimal place (tenths). Therefore, the hundredths place in 122.3 is effectively considered as "0" to match the decimal places of the first number. Upon aligning the decimal points, 38.15 and 122.3 indeed match as:

$\begin{array}{c} \hphantom{0}38.15 \\ - 122.30 \\ \end{array}$

4. This check confirms that there is an incorrect statement regarding "The position of the decimal point corresponds," as the numbers are aligned at the decimal points considering all decimal places are consistently represented.

Therefore, the statement "The position of the decimal point corresponds" is Not true.

Answer

Not true

Do you know what the answer is?

Question 1

Determine whether the exercise is correctly written or not.

Question 2

Determine whether the exercise is correctly written or not.

Question 3

Determine whether the exercise is correctly written or not.

The position of the decimal point corresponds.

Start practice

Decimal Fractions

Decimal Numbers

Meaning of the Decimal Number

Test yourself on decimal fractions - advanced!

Reduction and Amplification of Decimal Numbers

Addition and Subtraction of Decimal Numbers

Comparison of Decimal Numbers

Conversion of Decimal Number to Fraction

Conversion from Decimal Number to Mixed Number

Multiplication and Division of Decimal Numbers by 10, 100, etc.

Multiplication of Decimal Numbers

Division of Decimal Numbers

Repeating Decimal

Decimal Measurements

Density

Examples and exercises with solutions on decimal fractions

Exercise #1

Video Solution

Step-by-Step Solution

Answer

Exercise #2

Video Solution

Step-by-Step Solution

Answer

Exercise #3

Video Solution

Step-by-Step Solution

Answer

Exercise #4

Video Solution

Step-by-Step Solution

Answer

Exercise #5

Video Solution

Step-by-Step Solution

Answer

More Questions

All Operations in Decimal Fractions

Addition and Subtraction of Decimal Fractions

Decimal Fractions' Meaning

Reduction and Expansion of Decimal Fractions