The real line looks like this: a horizontal line in which small equidistant vertical lines are inserted.
Real number line
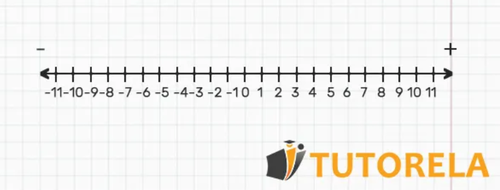
The real line looks like this: a horizontal line in which small equidistant vertical lines are inserted.

Characteristics of the number line:
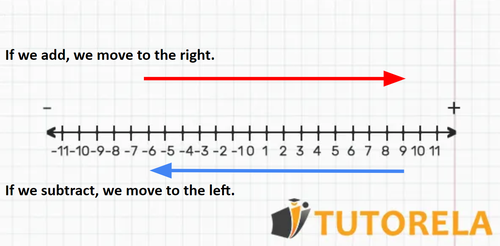
The operations of addition and subtraction can be seen as a horizontal movement on the number line.
All negative numbers appear on the number line to the left of the number 0.
To be more precise, we must point out that the number line is infinite. Therefore, when we refer to an image of the real line, we are referring to the image of a part of the whole line.
Decimal numbers can also be represented on the real line, for example:
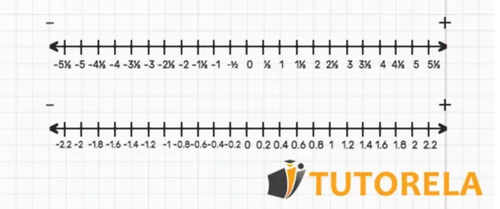
For example, let's look at the following two exercises that have already been solved:
Let us now focus on each of them and look at them as if they were a horizontal movement on the real line.

Every positive number is greater than zero
\( -2 < 0 \)
\( -3=-3 \)

\( 3.98 \) and \( +3.98 \) are two ways of writing the same number.
\( 4\frac{1}{2} < -5 \)
\( -4>-3 \)
Draw a number line starting with -8 and ending with 3. Then, reflect the following exercises on the number line using dots and arrows:
Observe the following real line and point out whether it is correct or not

If you are interested in this article you may also be interested in the following articles:
Positive numbers, negative numbers and zero
Elimination of parentheses in real numbers
Addition and subtraction of real numbers
Multiplication and division of real numbers
On the Tutorela blog you will find a variety of articles on mathematics.
\( 5 < -5 \)
The minus sign can be omitted
The sign is always written to the left of the number.

Consignee
What is the distance between and ?
Solution
Therefore the distance is skipped
Answer
What number appears at the red dot marked on the axis?

Solution:
By means of the axis we notice that the jumps between numbers are in multiplying the previous term by
Therefore
is the point
Answer
Does the number \( -6 \) appear on the number line to the right of number \( 2\text{?} \)
Fill in the corresponding sign
D ? J
What is the distance between A and K?

Query
Fill in the missing numbers
Solution
We note that the jumps between the numbers are at
Therefore
Answer
Request
According to the axis:

Solution:
We solve the exercise
Pay attention that minus multiplied by minus becomes plus.
Answer
What is the distance between D and I?
What is the distance between J and D?
All negative numbers appear on the number line to the left of the number 0.
Request
Solve according to the axis

Solution:
Solve the exercise
Pay attention that minus multiplied by minus becomes plus.
Answer
The number line or real line is a horizontal line divided into equidistant segments, i.e. at the same distance from each other, which serves to represent numbers in each segment, in which real numbers are indicated.
Every positive number is greater than zero
\( -2 < 0 \)
\( -3=-3 \)
The real line is a horizontal line where it is divided by intervals of the same distance, in these segments we can find the following elements:
It is called the number line or real line, since it contains all the real numbers, that is, the set of natural numbers, integers, rational numbers and irrational numbers, all these numbers are a subset of the real numbers, in other words, they are all the numbers.
\( 3.98 \) and \( +3.98 \) are two ways of writing the same number.
\( 4\frac{1}{2} < -5 \)
\( -4>-3 \)
On the number line we will place the positive numbers on the right side of zero and the negative numbers on the left side, so when we add we will move to the right side of the line, and when we subtract we will move to the left.
Task. Perform the following addition on the number line:
Solution: We locate the first term of the sum on the number line, and as we can observe it is a sum then, we are located at and we move segments to the right.
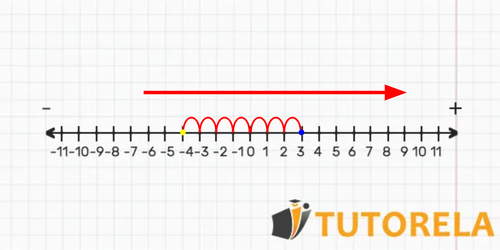
On the number line we can see that by going segments to the right we have fallen on the number , Therefore:
Result:
Task. Represent the following subtraction on a number line:
Solution:
We locate the minuend of the subtraction on the number line, then, we start at and then subtract the subtrahend, that is, the second term of the subtraction :
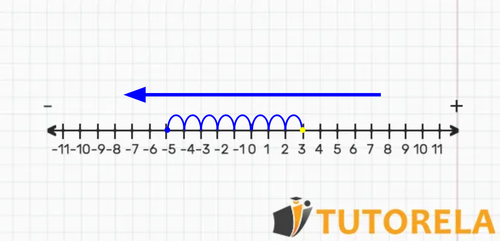
We observe that we have fallen in the , Using laws of signs less by more, will give us less, therefore this subtraction we can represent it as:
Therefore:
Result:
\( 5 < -5 \)
The minus sign can be omitted
The sign is always written to the left of the number.
All negative numbers appear on the number line to the left of the number 0.
If we draw a number line, we can see that to the right of zero are positive numbers, and to the left of zero are negative numbers:
Therefore, the answer is correct.
True.
Every positive number is greater than zero
The answer is indeed correct, any positive number to the right of zero is inevitably greater than zero.
True
Since every negative number is necessarily less than zero, the answer is indeed correct
True
and are two ways of writing the same number.
Indeed, both forms are identical since a number without a sign will be positive, as in the case of 3.98
If there is a plus sign before the number, the number is necessarily positive, as in the case of +3.98
Therefore, the answer is correct.
True
The answer is incorrect because a negative number cannot be greater than a positive number:
Not true