To convert a decimal fraction to a mixed fraction,
we ask ourselves how to read the decimal fraction or in other words, what the last digit represents –
if we use the word tenths – we place 10 in the denominator
if we use the word hundredths – we place 100 in the denominator
if we use the word thousandths – we place 1000 in the denominator
Converting a Decimal Fraction to a Mixed Number
Converting a decimal to a mixed number
The number itself – everything that appears after the decimal point, we place in the numerator.
The whole number in the decimal fraction, we add to the mixed fraction as the whole number in the mixed fraction.
Test yourself on converting decimal fractions to simple fractions and mixed numbers!
Write the following fraction as a decimal:
\( \frac{5}{100}= \)
Converting a decimal fraction to a mixed number
The transition from a decimal fraction to a mixed number is simple and easy if you just know the right way.
To do it correctly without making mistakes, we recommend that you make sure you know how to read decimal fractions properly.
If you know how to read decimal fractions correctly – the path to success in transitioning from a decimal fraction to a simple fraction is completely paved for you.
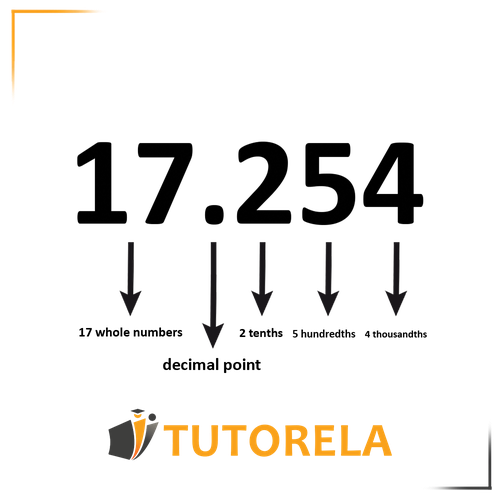
How do you read a decimal fraction?
A decimal fraction represents a fraction or a non-whole number using a decimal point.
The decimal point divides the fraction as follows:

Explanation:
The entire part to the left of the decimal point is called whole numbers.
The entire part to the right of the decimal point is divided as follows:
The first digit after the point represents tenths
The second digit after the point represents hundredths
The third digit after the point represents thousandths
Remember! There is no unity – the counting starts from tenths.
How do we know the denominator of the mixed fraction?
As we saw above, decimal fractions consist of whole numbers that are before the decimal point and parts that are after the decimal point, where the parts are made up of tenths, hundredths, and thousandths.
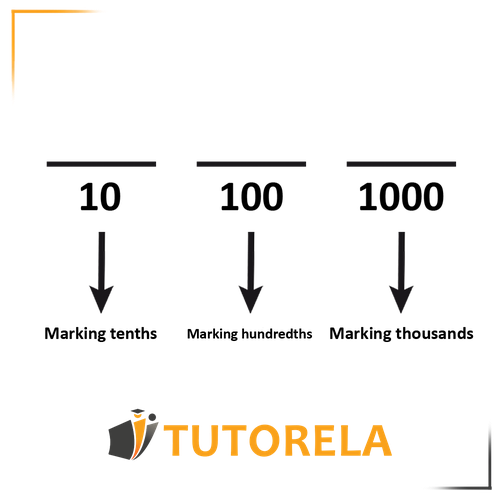
If we convert the tenths, hundredths, and thousandths to a denominator in a simple fraction, we get:
Remember:
Thousandths – 1000 in the denominator
Hundredths – 100 in the denominator
Tenths – 10 in the denominator
How will you remember this?
It is very easy and simple.
Tenths come from the word 10, so the denominator that should appear is 10.
Hundredths come from the word 100, so the denominator that should appear is 100.
Thousandths come from the word 1000, so the denominator that should appear is 1000.
The key to success lies here:
To read a decimal fraction correctly, we need to ask ourselves what the last digit in the decimal fraction represents.
For example:
How do we read the decimal ?
6 is the last digit and it represents hundredths, so we read the decimal as whole and hundredths.
How wonderful! We just learned the notation for hundredths -

All that remains for us is to put in the numerator, in the whole number part and get the simple fraction of the decimal :
Let's practice more:
Convert the decimal to a mixed number
Solution:
Let's ask ourselves – how do we read the fraction?
wholes and tenths.
Therefore, we will use the tenths notation (denominator ) and place in the numerator and in the wholes:
Convert the decimal fraction to a simple fraction
Solution:
Let's ask ourselves – how do we read the fraction?
wholes and thousandths.
Therefore, we will use the thousandths notation (denominator ), place in the numerator and as the whole number:
Note – if the fraction can be simplified, you can simplify it without changing its value:
And indeed we already know that:
Convert the decimal to a simple fraction
Solution:
Let's ask ourselves – how do we read the fraction?
whole and hundredths
Therefore, we will use the hundredths notation – denominator , place in the numerator and as the whole number.
We get:
We can simplify by dividing by and get:
Another example
Convert the decimal to a mixed number
Solution:
Let's ask ourselves – how do we read the fraction?
wholes and hundredths
Therefore, we will use the hundredths notation - denominator and place in the numerator. Let's not forget to add wholes on the side and we get:
Write the following fraction as a decimal:
\( \frac{3}{100}= \)
Write the following fraction as a decimal:
\( \frac{3}{100}= \)
Write the following fraction as a decimal:
\( \frac{11}{100}= \)
Examples with solutions for Converting Decimal Fractions to Simple Fractions and Mixed Numbers
Exercise #1
Write the following fraction as a decimal:
Video Solution
Step-by-Step Solution
Let's write the simple fraction as a decimal fraction
Since the fraction divides by 100, we'll move the decimal point once to the left and get:
We'll add the zero before the decimal point and get:
Answer
0.05
Exercise #2
Write the following fraction as a decimal:
Video Solution
Step-by-Step Solution
Let's write the simple fraction as a decimal fraction
Since the fraction divides by 100, we move the decimal point once to the left and get:
We'll add the zero before the decimal point and get:
Answer
0.03
Exercise #3
Write the following fraction as a decimal:
Video Solution
Step-by-Step Solution
Let's write the simple fraction as a decimal fraction
Since the fraction divides by 100, we move the decimal point once to the left and get:
We'll add the zero before the decimal point and get:
Answer
0.03
Exercise #4
Write the following fraction as a decimal:
Video Solution
Step-by-Step Solution
Let's write the simple fraction as a decimal fraction
Since the fraction divides by 100, we move the decimal point once to the left and get:
We'll add the zero before the decimal point and get:
Answer
0.11
Exercise #5
Write the following fraction as a decimal:
Video Solution
Step-by-Step Solution
Let's write the simple fraction as a decimal fraction
Since the fraction divides by 100, we move the decimal point once to the left and get:
We'll add the zero before the decimal point and get:
Answer
0.19









