Mixed Numbers and Fractions Greater Than 1

In this article, we will learn everything necessary about mixed numbers and fractions greater than $1$.
We will learn how to convert everything to a fraction, subtract, add, multiply, and compare. All in an easy and efficient way.

A mixed number is a number made up of a whole number and a fraction - hence its name - it combines whole numbers and fractions.
Examples of mixed numbers:
$2\frac {3}{5}$, $1\frac {1}{2}$, $4\frac {2}{3}$

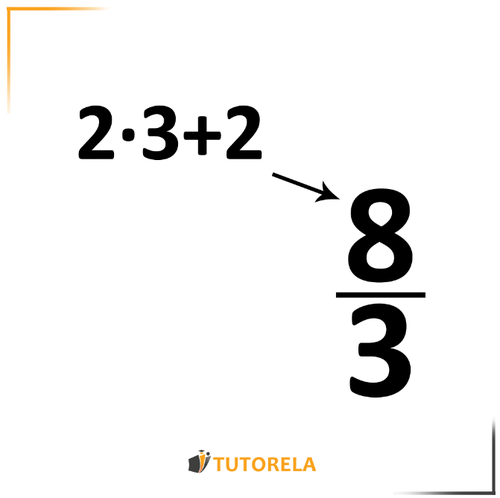
Let's look at this mixed number $2\frac {2}{3}$
To find the numerator we multiply the whole number by the denominator. To the product obtained we add the numerator.
Nothing is modified in the denominator.

We will obtain:

First, let's see what a fraction equivalent to $1$ looks like.
A fraction equivalent to $1$ is one whose numerator and denominator are equal. For example, $2 \over 2$ or $4 \over 4$.
A fraction greater than $1$ is a fraction whose numerator is larger than the denominator.
Whenever the numerator is larger than the denominator, the fraction will be greater than $1$. For example, $3 \over 2$

Observe:

Every mixed number is greater than $1$ and we can write it in the form of a fraction that is greater than $1$.

Practice:
Convert the mixed number $3 \frac {2}{9}$ to a fraction greater than $1$.
Solution:
We will multiply the whole number by the denominator and add the numerator to the product. We will write the result in the numerator
$3 \times 9+2=29$
The denominator will not be altered.
We obtain:
$29 \over 3$
It is clear that the fraction obtained is greater than $1$ –> the numerator is larger than the denominator.

In certain cases, when we want to find out the number of units or just to order the final result, we prefer to convert a fraction greater than $1$ to a mixed number.

We will do it in the following way:
We will calculate how many whole times the numerator fits into the denominator - this will be the whole number.
What remains, we will write in the numerator, and the denominator will remain unchanged (does not change).
Let's learn by practicing:
Here is a fraction greater than $1$:
$27 \over 7$
To convert it to a mixed number we will divide the numerator by the denominator. Let's ask ourselves how many whole times $7$ fits into $27$ ?
We will obtain:
$27:7=3…….$
3 times -> this will be the whole number of the result. 

Now let's see what remains to complete the numerator $27$.
What is the remainder?
$3 \times 7=21$
$27-21=6$

We have a remainder of $6$, that is what is placed in the numerator.
The final result is:
$\frac {27}{7}=3\frac {6}{7}$

When we talk about addition and subtraction of fractions, the first step is to convert everything to fractions (without whole numbers).
This way we can reach the common denominator and then add or subtract the numerators.

$\frac {5}{2}+1\frac {2}{3}=$
Solution:
Given this addition exercise with a fraction larger than $1$ and a mixed number.
The first step is to convert the mixed number to a fraction in the way we have learned before.
It will give us:​ $1\frac {2}{3}=\frac {5}{3}$

Let's rewrite the exercise:

Now we will find the common denominator by multiplying the denominators and we will get:
$\frac {15}{6}+\frac {10}{6}=\frac {25}{6}$
We can convert the result to a mixed number like this:
$4\frac {1}{6}$

When we talk about multiplication and division, indeed, there is no need to find the common denominator, but it is necessary to convert mixed numbers into fractions.
This way, the operations will be carried out easily.

Comparison between a mixed number and a fraction greater than $1$
To be able to compare a mixed number and a fraction greater than $1$,
The first thing we must do is, clearly, convert the mixed number to a fraction -> that is, a fraction with numerator and denominator.
Then, find the common denominator, only after this can we compare the numerators.

Let's practice:
Mark the corresponding sign $<,>,=$
$\frac {23}{36}$_______________$2\frac {5}{7}$

Solution:
We will convert the mixed number to a fraction and rewrite the exercise.
We will obtain:

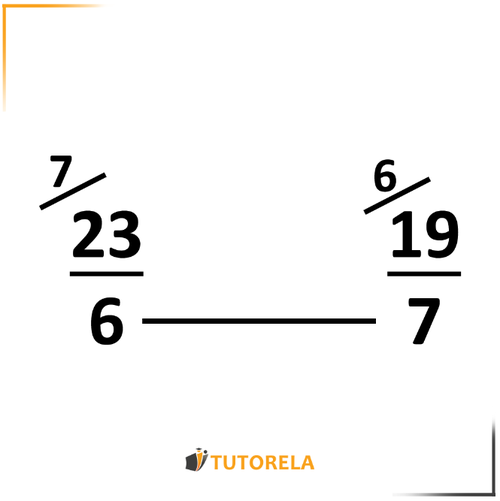
We will find the common denominator by multiplying the denominators and we will obtain:
$\frac {161}{42}$_______>________$\frac {114}{42}$