Part of a quantity

The topic of a part of a quantity in fractions is pleasant and easy if you understand the principle and logic.
Therefore, focus and see how you learn to solve questions about a part of a quantity without any problem.
In everyday life, a whole quantity can be the number of children in a class for example, and a part of a quantity is the number of children studying in a specific class.

We divide the topic into 3 situations.

The total amount is known
and we want to know something specific about a part of the amount.
Procedure:
We will divide the total amount by the denominator of the part.
We will multiply the result obtained by the numerator of the part and we will get the final answer.

Let's see this while asking a question:
In the music class there are $30$ students - this is the total amount.
$1 \over 3$ Of the class plays the guitar - that is the specific part.

How many children in the music class play the guitar? – the part of the total amount.

Solution:
to know how much is $1 \over 3$
We will divide the total amount -> $30$ by the number $3$ (The number that appears in the denominator of the part.
We will get:
$30:3=10$
If we multiply $10$ by the numerator of the part -> $1$ we still get, $10$.

That is $1 \over 3$ of $30$ is $10$ children.
We can also see this in the illustration:

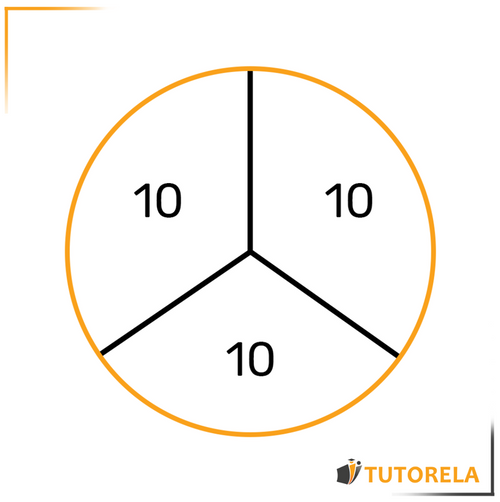
When we divide $30$ by $3$ into equal parts, we get that each part is equal to $10$.
This means that-> $10$ children in the class play the guitar.

Bonus section:  
$2 \over 3$ of the music class play the drums.
How many children play the drums?

Solution:
Now we want to know how much is $2 \over 3$ of $30$
We found out that $1 \over 3$ of $30$ is $10$ children and therefore $2 \over 3$ of $30$ is $20$ children. That is $20$ children play the drums.
The main way without depending on the first section:
We will divide the total amount - $30$ By the denominator of the part -> $3$
We get
$30:3=10$
The result $10$ we got, we multiply by the numerator of the part -> $2$
We get
$10 \times 2=20$

Answer:
That is $20$ children play the drums.

The total amount is unknown
A part of an amount is known and given in a number (it is called partial amount).

The procedure is:
we will divide the given number (partial amount) by the numerator of the part.
We will multiply the result by the denominator of the part and obtain the total amount.

$6$ students in the class wear a red shirt and make up $2 \over 5$ of the class.
How many children are in the class?

Solution:
here we need to find the total amount, so we will solve it according to the previous steps.
We will divide the given number (the partial amount) –> $6$ by the numerator of the fraction $2$ and we get:
$6:2=3$
The result we obtained $3$ we multiply by the denominator of the fraction - $5$ and we will get the total amount.
We get:
$3 \times 5=15$

Answer:
There are $15$ students in total in the class.

The total amount is known
The partial amount (the given number) is known
The part in the fraction is unknown

The procedure is:

We will divide the partial amount by the total amount - using a fraction.

That is:

In the numerator - we will note the partial amount
In the denominator - we will note the total amount
The fraction we obtained, we will reduce and obtain the desired part.

$7$ children in the class can speak English.
There are a total of $42$ children in the class.
What part of the class can speak English?

Solution:
We will write the partial amount in the numerator $7$
and in the denominator we will write the total amount $42$
We obtain:
$7 \over 42$
We reduce and obtain:
$1 \over 6$
Answer:
$1 \over 6$ of the students in the class can speak English.