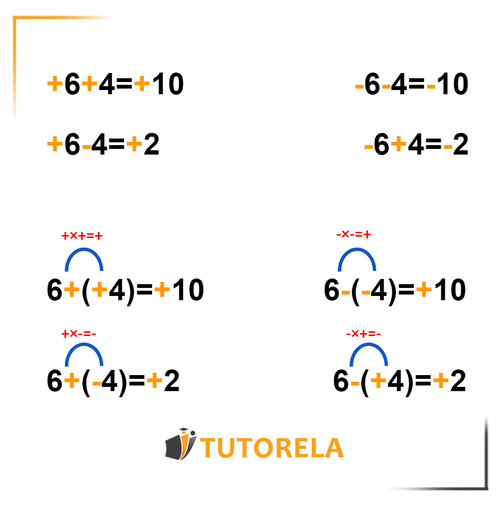
After studying real numbers, it's time to learn how to use them in an equation. Initially, our goal with equations is to simplify them to make it easier to solve problems, and we do this by grouping operations and adding and subtracting real numbers. We just need to remember two rules:
- When the mathematical operation and the sign of the following real number are of the same type, we group them into a sum.
- For example: 5+(+5) / 5−(−5)
5+5 will become
- When the mathematical operation and the sign of the following real number are of different types, we group them into an operation that will give the difference between them. For example: 5+(−5) / 5−(+5)
5−5 will become
For example:
10+(+5)−(+3)−(−6)+(−8)=
10+5−3+6−8=10
There is a very well-known tactic that helps to understand the topic of real numbers in the best way, it's called the elevator method and it serves to clarify the addition and subtraction of real numbers. With this method, we imagine that the exercise is like a journey in an elevator that goes through the floors. Observe the following exercise:
−5−(+1)−(−8)+(−3)=
Before using the elevator method we have to group the signs to simplify the exercise
−5−1+8−3=
Now look at the first number. In fact, you start the exercise on floor -5 and now you are asked to go down one floor. This way you reach floor -6.
Now you are asked to go up 8 floors. So, if we were on floor -6 we will arrive at floor 2. Finally, you are asked to go down 3 floors, therefore, you end up on floor -1, which is the result of the exercise
−5−1+8−3=−1
We will give consistency to the principles outlined through the following examples:
(+3)+(+4)+(+5)=3+4+5=+12
(−3)+(−4)+(−5)=−3−4−5=−12
−10+2=−8
6−20=−14
(−10)−(−100)=−10+100=90
8+(−4)=8−4=4
Assignment
−27−(−7)+(−6)+2−11=
Solution
First, we resolve the points that have a plus or minus sign before another sign.
−27+7−6+2−11=
Now we solve it as a common exercise:
−27+7−6+2−11=−35
Answer
−35
Assignment
?−(−12)=−40
Solution
First, let's note that the two minuses turn into a plus.
?+12=−40
We will move the 12 to the right side
?=−40−12
Finally, we solve
?=−52
Answer:
−52
Assignment
−36+6=
Solution
We use the laws of addition and subtraction to solve accordingly.
−36+6=−30
Answer:
−30
12−(−2)=
Solution
Pay attention to the fact that the minus and minus signs become plus, and we solve the exercise accordingly.
12+2=14
Answer
14
Assignment
Given:
a Negative number
b Negative number
What is the sum of a+b?
Solution
When we add two negative numbers, the result we will obtain is a negative number.
Answer
Negative