Sum and Difference of Angles

Even if angles don't have any numbers, we'll learn how to represent their sum or difference and arrive at the correct result: the correct naming of the angle we get as a result.
Don't worry, the sum and difference of angles is not a difficult topic and mainly relies on the representation of the angles.
Don't know how to correctly mark angles? Go practice representing angles and come back with 90% success!

Let's look at the following example

We can say that:

$∡BAE+∡EAC=∡BAC$

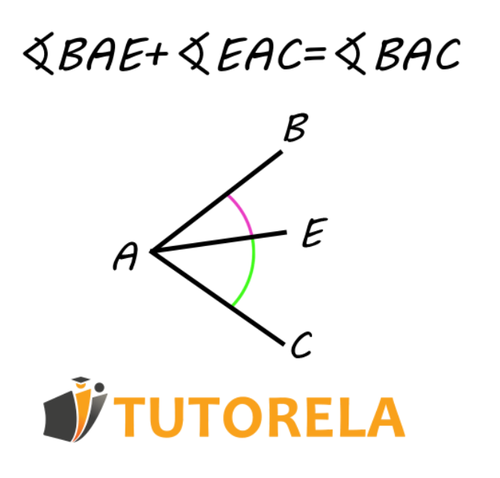
It is known that the whole is composed of the sum of its parts, and the same is true with angles.
The large angle A) is made up of the two angles it contains.
If we add the 2 angles that make up angle A), we will obtain this angle.

If we know the size of the angles, we can, with a simple mathematical operation, discover the real value of angle A).

For example, having the following:
$∡BAC=30°$

$∡EAC=35°$

and we were asked to calculate: $∡BAC$
which is actually the large angle A) that contains the two given angles inside,
all we have to do is add the values of the given angles and find the one we were asked to discover.

We can say that:
$∡BAC=30°+35°=65°$

Just as we have added angles, we can also subtract one angle from another.
Let's look at the following example:
If we know that:

$∡BAC=65°$
$∡BAE=30°$

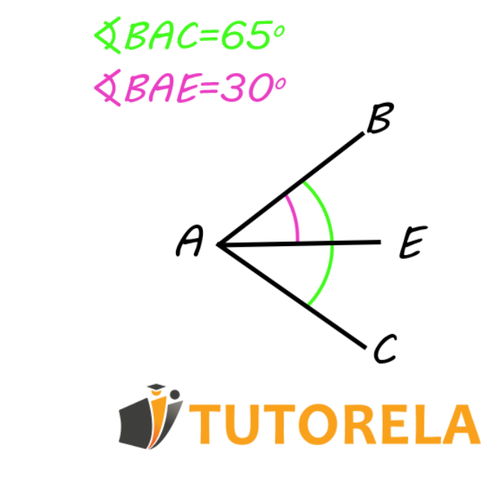
What will be the value of $∡EAC$?

Since angle $∡BAC$ contains the angles $∡BAE$ and $∡EAC$ and is composed only of these two,
we can subtract the given angle $∡BAE$ from the larger angle $∡BAC$ to find the angle $∡EAC$.
That is:

$∡EAC=65-30=35$
$∡EAC=35°$

Remember: The whole is composed of the sum of its parts!
We can add and subtract angles that are on the same vertex without any problem.
Just pay attention to do it the right way and know how to read the names of the angles.

Assignment

Calculate the value of $X$

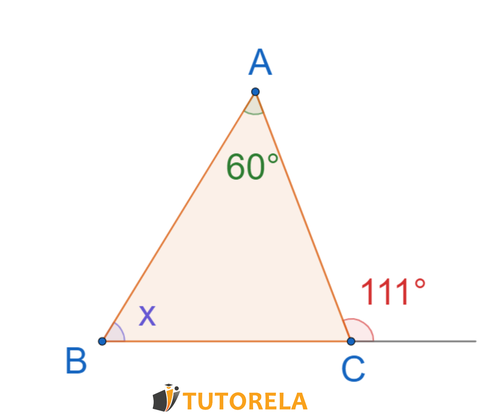
Solution

We calculate $\sphericalangle ACB$

$\sphericalangle ACB=180-111=69$

Now we calculate $\sphericalangle ABC$

Remember that the sum of all angles in a triangle equals $180^o$

$\sphericalangle ABC=180-69-60=51$

Answer

$51$

Assignment

Given the angles between parallel lines in the graph, what is the value of: $x$?

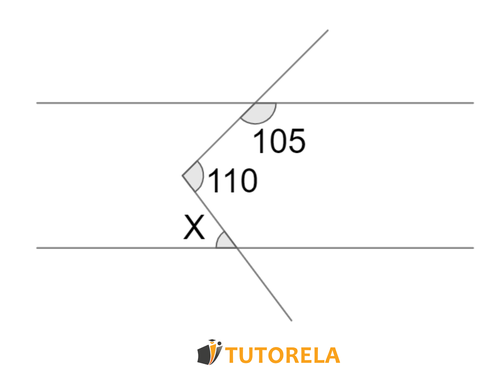
Solution

$X=?$

$180^o-105^o=75^o$

$75^o+X=110^o$ $/-75^o$

$X=110^o -75^o$

$35^o$

Answer

$35^o$

Prompt

Given the parallel lines $a,b$

Find the angle $\alpha$

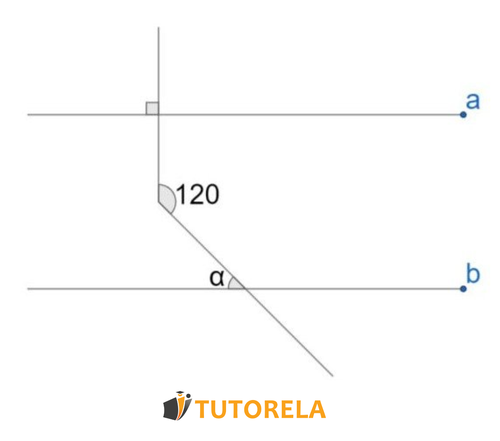
Solution

We extend the vertical line to the end and label the adjacent angles $\beta$ and: $\gamma$ with $\beta$ on the left and: $\gamma$ on the right

Now we notice that the angle $\beta$ is a corresponding angle to: $90^o$ and since adjacent angles sum up to: $180^o$, then the angle $\gamma$ is also equal to: $90^o$

The remaining angle in the small triangle we created, which is also adjacent to: $120^o$ is called $\delta$

As it is adjacent to: $120^o$ it will be equal to: $60^o$ since it is complementary to: $180^o$

Now we calculate the sum of angles in the small triangle:

$180=\alpha+\gamma+\delta$

We replace with the data we know

$180=\alpha+90+60$

$180=\alpha+150$

We move the terms

$\alpha=180-150$

$\alpha=30$

Answer

$30$

Assignment

$\triangle ABC$ is a triangle

Based on the information, what is the size of the angle $\sphericalangle BAD$

of value $X$?

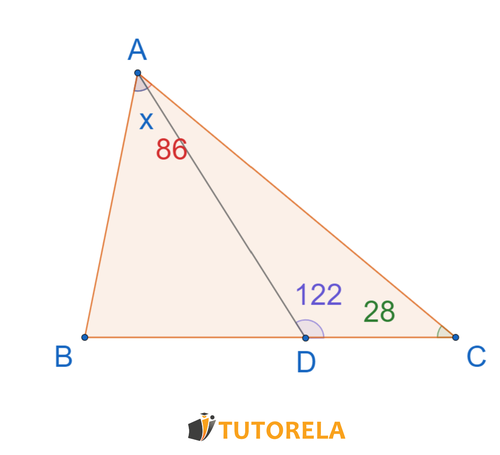
Solution

First, we calculate the angle $\sphericalangle B$

$\sphericalangle B=180-28-86=66$

Now let's find the angle $\sphericalangle ADB$

$\sphericalangle ADB=180-122=58$

Now we refer to the triangle $\triangle ABD$

$\sphericalangle BAD=180-66-58=56$

Answer

$56$

Assignment

Calculate the values of $Y$ and $X$

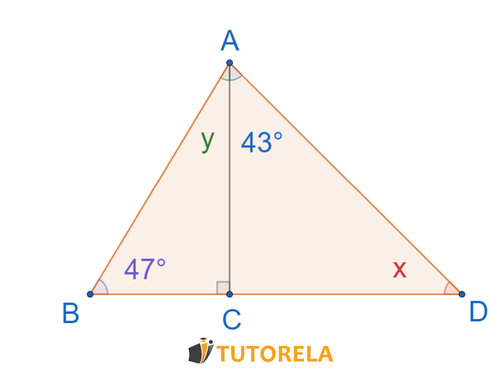
Solution

We refer to triangle $\triangle ABC$

Let's find the angle $Y$

$\angle Y=180-47-90=43$

Now we refer to triangle $\triangle ACD$

Let's find the angle $X$

$\angle X=180-90-43=47$

Answer

$Y=43, X=47$