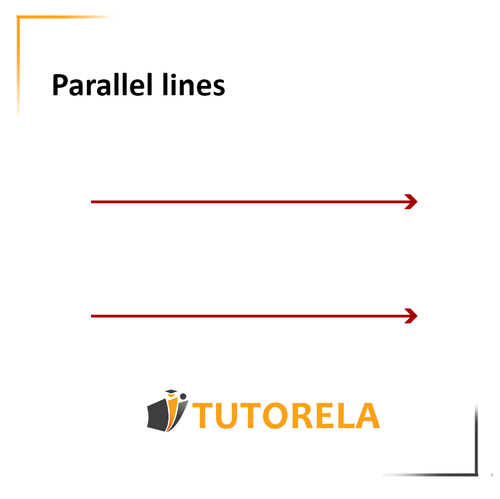
Parallel lines are two straight lines that will never meet. They are on the same plane and will never intersect.
Parallel and Perpendicular Lines
Parallel and Perpendicular Lines
Parallel lines
They are commonly marked with a symbol that looks like this:
Perpendicular lines
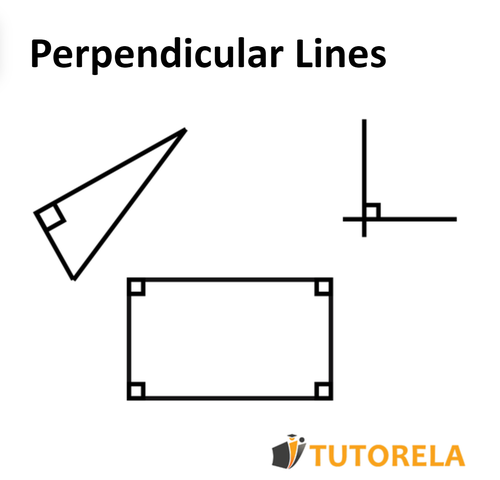
Perpendicular lines are lines that are perpendicular to each other and form a right angle of degrees between them.
Angles in parallel lines
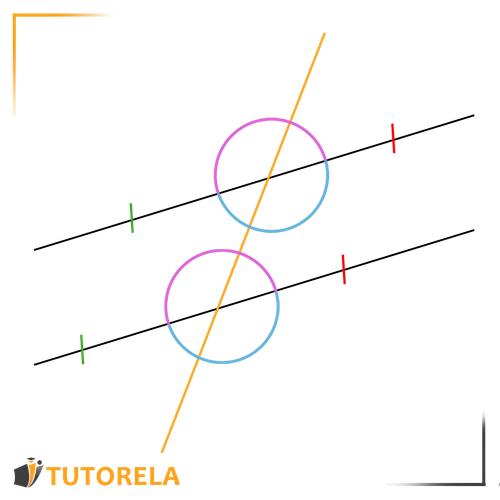
Angles in parallel lines are angles formed when a third line intersects the two given parallel lines.
To classify the angles created by the intersection, we need to identify if they are:
- Above the line - the pink part
- Below the line - the light blue part
- Right of the line - the red part
- Left of the line - the green part
Parallel and Perpendicular Lines
Parallel lines
Parallel lines are two straight lines that will never meet. They are on the same plane and will never intersect.
They are commonly marked with a symbol that looks like this:
Try to imagine a straight path leading from infinity to infinity. The edges of the path will never meet, like parallel lines.

Meet the properties of parallel lines:
- The distance between all points on one parallel line to the second parallel line is identical
- The slopes of parallel lines are identical - meaning their steepness - how much they are inclined up and down is the same in both - this is what causes them to never meet or intersect.
If we look closely, we can identify that parallel lines form various different shapes such as parallelogram, rhombus, square, and rectangle.
Click here to learn more about parallel lines
Perpendicular lines
Perpendicular lines are lines that are at right angles to each other and form a right angle of degrees between them.
Upon closer inspection, we can identify that perpendicular lines make up a wide variety of geometric shapes such as squares, rectangles, and right triangles.

Angles in parallel lines
Angles in parallel lines are angles created when a third line intersects the two given parallel lines.
To classify the angles created by the intersection, we need to identify if they are:
- Above the line - the pink part
- Below the line - the light blue part
- Right of the line - the red part
- Left of the line - the green part

Try to think of it as 2 buildings adjacent to each other. In these buildings, angles reside.
In order to classify them, you need to identify the side and floor of each angle.
Corresponding angles
• Located on the same side of the transversal line
• Located on the same "level" relative to the line
The property - corresponding angles between parallel lines are equal.
Below is an example of corresponding angles:
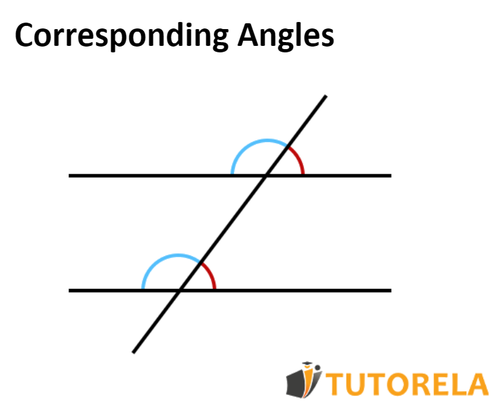
The two marked angles are located on the left side and on the bottom floor - therefore they can be considered as corresponding and equal.
- Both are on the same side and on the same floor.
Vertical angles
• Share a common vertex - located on the same vertex
• Located opposite to each other
The property - vertical angles between parallel lines are equal.
Here are examples of vertical angles:
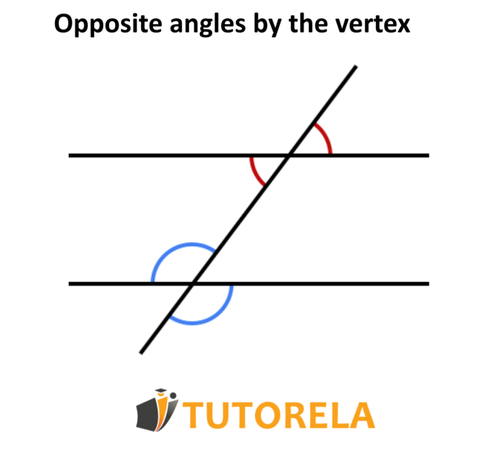
The two marked angles are located on the same vertex and are opposite to each other, therefore they are vertical angles.
They share the same vertex.
Adjacent angles
• Adjacent to each other
• Located on the same line
The property - The sum of adjacent angles between parallel lines equals 180°.
Below is an example of adjacent angles:
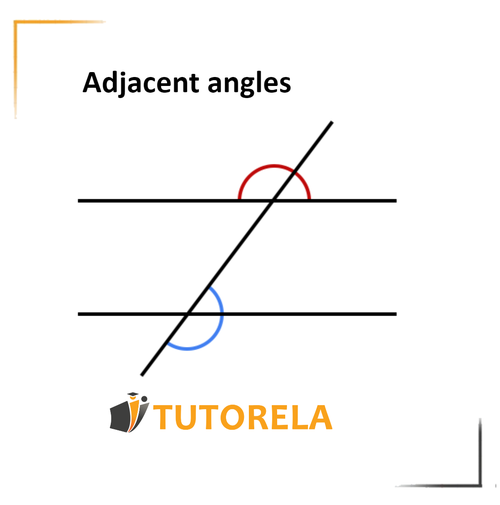
The two marked angles are on the same line - orange and are adjacent to each other, therefore they are adjacent angles.
Alternate angles
• Not located on the same side of the intersecting line
• Not located on the same "level" in relation to the line
The property - alternate angles between parallel lines are equal.
Below is an example of alternate angles:
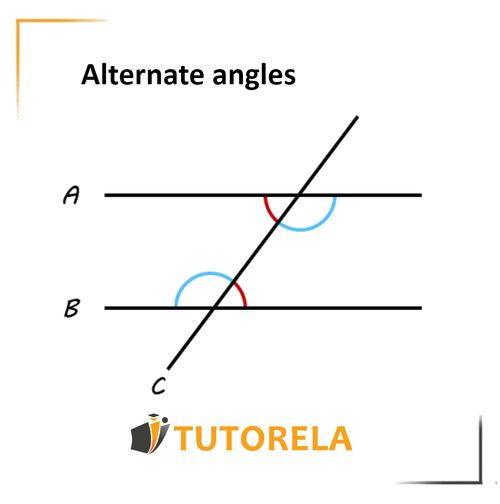
The two marked angles are not on the same floor and not on the same side, therefore they are alternate angles.
The first angle in building A is on the right side on the upper floor, while the second angle in building B is on the left side on the lower floor.
One-sided angles
• Located on the same side of the transversal line
• But not on the same "level" in relation to the line
The property - The sum of corresponding angles between parallel lines equals 180°.
Here are examples of one-sided angles:
The two marked angles are not on the same floor but are on the same side, therefore they are corresponding angles.
The first angle in building A is on the right side on the upper floor, while the second angle in building B is on the right side on the lower floor.
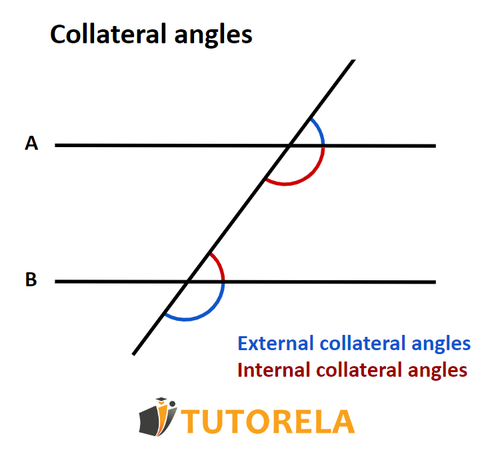
Note - The red angles in the figure above are exterior alternate angles due to the fact they are located on the outer side of the parallel lines.
Interior alternate angles are located on the inner side of the parallel lines:
- Area
- Trapezoids
- Area of a trapezoid
- Perimeter of a trapezoid
- Parallelogram
- The area of a parallelogram: what is it and how is it calculated?
- Perimeter of a Parallelogram
- Proving Parallel Lines
- Rectangle
- Calculating the Area of a Rectangle
- The perimeter of the rectangle
- Congruent Rectangles
- The sides or edges of a triangle
- Triangle Height
- The Sum of the Interior Angles of a Triangle
- Exterior angles of a triangle
- Perimeter
- Triangle
- Types of Triangles
- Obtuse Triangle
- Equilateral triangle
- Identification of an Isosceles Triangle
- Scalene triangle
- Acute triangle
- Isosceles triangle
- The Area of a Triangle
- Area of a right triangle
- Area of Isosceles Triangles
- Area of a Scalene Triangle
- Area of Equilateral Triangles
- Perimeter of a triangle
- Areas of Polygons for 7th Grade
- Right Triangle
- Area of a right-angled trapezoid
- Area of an isosceles trapezoid
- Median in a triangle
- Center of a Triangle - The Centroid - The Intersection Point of Medians
- How do we calculate the area of complex shapes?
- How to calculate the area of a triangle using trigonometry?
- How do we calculate the perimeter of polygons?
- All terms in triangle calculation








