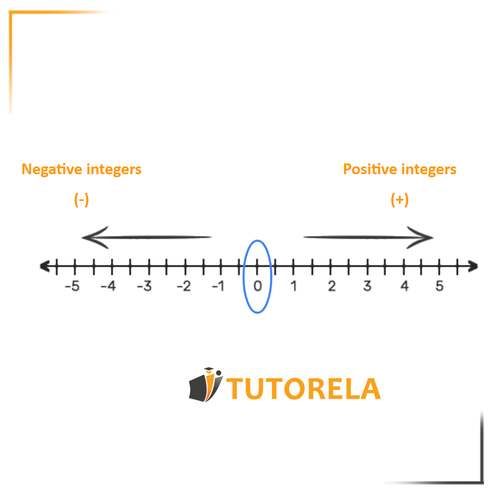
We learned in the previous article about the number line AND we also talked about positive and negative numbers. In this article we move on and call them integers.
Integers
What are integers?
The term "integer" refers to any number to the left of which there is a plus sign (+) or minus sign (-).
- The plus sign ( ) indicates that the number is positive (greater than zero). The minus sign (-) means that the number is negative (less than zero).
- When a number appears without one of these two signs, it means that the number is positive.
- Exception: The number . Zero is the only number that is neither positive nor negative. It is possible to write "" or "", but in this case the signs will have no meaning.
Test yourself on signed numbers (positive and negative)!

What will be the sign of the result of the next exercise?
\( (-16)\cdot(-5)= \)
Examples:
Depending on the location of numbers on the number line, the following rules can be determined:
- A positive number is always larger than a negative number.
- If we have two positive numbers, the number whose absolute value is larger will be the larger number.
- If we have two negative numbers, the number whose absolute value is smaller will be the smaller number.
Exercises with integers
Exercise 1
Write in the blank one of the following signs:
- __
- __
- __
- __
- __
What will be the sign of the result of the next exercise?
\( (-2)\cdot(-4)= \)
What will be the sign of the result of the next exercise?
\( (-3)\cdot(-4)= \)
What will be the sign of the result of the next exercise?
\( (-2)\cdot(-\frac{1}{2})= \)
Exercise 2
Read the following sentences, and determine which one is true or false:
- Every positive number is greater than zero.
- The negative sign can be omitted.
- The sign is always written to the left of the number.
- "" and "" are two ways of writing the same number.
- The number appears on the number line to the right of the number .
- All negative numbers appear on the number line to the left of the number .
- The number is smaller than the number .
Exercise 3
Question
What is the value we will have to input to solve the following equation?
Solution
To answer this question it is possible to answer in two ways:
One way is replacement:
We place power of and it seems that we have arrived at the correct result, ie:
Another way is by using the root
That is
Answer:
Determine the resulting sign of the following exercise:
\( \frac{1}{4}\cdot\frac{1}{2}= \)
Will the result of the exercise below be positive or negative?
\( 5\cdot(-\frac{1}{2})= \)
What will be the sign of the result of the next exercise?
\( (-4)\cdot12= \)
Exercise 4
Question
What is the result of the following power?
To solve this question we must first understand the meaning of the exercise.
Now everything is simpler... Correct?
We obtain:
Answer
Exercise 5
Task
Solution
Pay attention that minus multiplied by minus becomes plus, and therefore
Answer
What will be the sign of the result of the next exercise?
\( (-6)\cdot5= \)
What will be the sign of the result of the next exercise?
\( 6\cdot3= \)
What will be the sign of the result of the next exercise?
\( 2\cdot(-2)= \)
Exercise 6
Task
Solution
First we put the signs in order.
Now we solve as a common exercise:
Answer
Exercise 7
Task
Given that:
Negative number
Negative number
What is the sum of ?
Solution
When we add two negative numbers, the result we will get will be a negative number.
Answer
Negative
If you are interested in this article you may also be interested in the following articles:
Positive numbers, negative numbers and zero
Elimination of parentheses in real numbers
Addition and subtraction of real numbers
Multiplication and division of real numbers
On the Tutorela blog you will find a variety of articles on mathematics.
Fill in the missing number:
\( (-2)\cdot?=-4 \)
Fill in the missing number:
\( (-6)\cdot?=-12 \)
Fill in the missing number:
\( (-3)\cdot?=-9 \)
Review questions
What are integers?
Whole numbers can be written without a decimal point and never with a fraction, for example are not whole numbers. Therefore, integers are positive numbers, negative numbers (without decimal) and zero.
For example:
i.e. the natural numbers with their respective negatives.
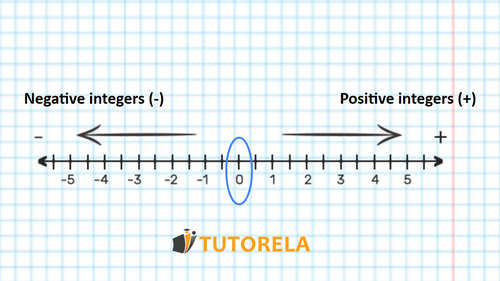
How to order integers?
The integers can be placed on the number line in the following way:
There are rules to be able to count integers, let's look at the case of addition:
- If we add two positive integers, we only add the absolute values and keep the positive sign.
Example 1
Both numbers are positive and the result is still positive.
- When adding negative numbers they are added together and the result is still negative.
Example 2
The absolute values are added, but the result is still negative.
- When we have numbers with different signs they are subtracted, that is to say, we subtract the smaller number from the larger number and the result will have the sign of the number with the larger absolute value.
Fill in the missing number:
\( 2\cdot?=-8 \)
Fill in the missing number:
\( 10\cdot?=-100 \)
What will be the sign of the result of the next exercise?
\( (-16)\cdot(-5)= \)
Example 3
In this operation we can see that we have numbers with different signs, so we subtract them and we will put the sign of the bigger number, in this case the result is negative.
Here we subtract the smaller number from the bigger number and in this case the result will be positive because the bigger number has a positive sign.
What is an integer, simply?
An integer is a neative OR positive whole number that does not have any decimal point or a number that cannot be written as a fraction.
What will be the sign of the result of the next exercise?
\( (-2)\cdot(-4)= \)
What will be the sign of the result of the next exercise?
\( (-3)\cdot(-4)= \)
What will be the sign of the result of the next exercise?
\( (-2)\cdot(-\frac{1}{2})= \)
Which numbers are not integers?
Decimal numbers, rational numbers and irrational numbers are not integers, such as:
Determine the resulting sign of the following exercise:
\( \frac{1}{4}\cdot\frac{1}{2}= \)
Will the result of the exercise below be positive or negative?
\( 5\cdot(-\frac{1}{2})= \)
What will be the sign of the result of the next exercise?
\( (-4)\cdot12= \)
Examples with solutions for Signed Numbers (Positive and Negative)
Exercise #1
What will be the sign of the result of the next exercise?
Video Solution
Step-by-Step Solution
To determine the sign of the expression , we follow these logical steps:
- Step 1: Identify the signs of the numbers involved. Both numbers and are negative.
- Step 2: Apply the rule for multiplication of signed numbers: The product of two numbers with the same sign (both negative) is always positive.
Therefore, the sign of the result for the expression is Positive.
Answer
Positive
Exercise #2
What will be the sign of the result of the next exercise?
Video Solution
Step-by-Step Solution
It's important to remember: when we multiply a negative by a negative, the result is positive!
You can use this guide:
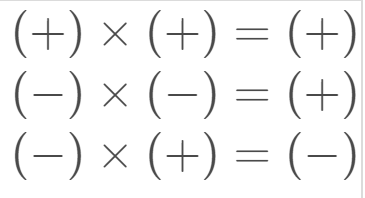
Answer
Positive
Exercise #3
What will be the sign of the result of the next exercise?
Video Solution
Step-by-Step Solution
Let's remember the rule:
Therefore, the sign of the exercise result will be positive:
Answer
Positive
Exercise #4
What will be the sign of the result of the next exercise?
Video Solution
Step-by-Step Solution
Let's recall the law:
Therefore, the sign of the exercise result will be positive:
Answer
Positive
Exercise #5
Determine the resulting sign of the following exercise:
Video Solution
Step-by-Step Solution
When there is no minus or plus sign before the numbers, we usually assume that these are positive numbers as shown below:
(+1/4)*(+1/2)=
The dot in the middle represents multiplication:
So the question in other words is - what happens when we multiply two positive numbers together?
We know that two positive integers when multiplied result in a positive integer:
Therefore the answer is "positive".
Answer
Positive
More Questions
All Operations in Signed Numbers
Signed Numbers (Positive and Negative)
- The Order of Basic Operations: Addition, Subtraction, and Multiplication
- Order of Operations: Exponents
- Order of Operations: Roots
- Division and Fraction Bars (Vinculum)
- The Numbers 0 and 1 in Operations
- Neutral Element (Identiy Element)
- Order of Operations with Parentheses
- Order or Hierarchy of Operations with Fractions
- Multiplicative Inverse
- Advanced Arithmetic Operations
- The commutative property
- The Commutative Property of Addition
- The Commutative Property of Multiplication
- The Associative Property
- The Associative Property of Addition
- The Associative Property of Multiplication
- The Distributive Property
- The Distributive Property for Seventh Graders
- The Distributive Property of Division
- The Distributive Property in the Case of Multiplication
- Subtracting Whole Numbers with Addition in Parentheses
- Division of Whole Numbers Within Parentheses Involving Division
- Subtracting Whole Numbers with Subtraction in Parentheses
- Division of Whole Numbers with Multiplication in Parentheses
- The commutative properties of addition and multiplication, and the distributive property
- Exponents and Roots - Basic
- What is a square root?
- Square Root of a Negative Number
- Exponents and Exponent rules
- Basis of a power
- The exponent of a power
- Powers
- Order of Operations - Exponents and Roots
- Special cases (0 and 1, reciprocals, fraction line)









