Solving Equations by Multiplying or Dividing Both Sides by the Same Number

Multiplying or Dividing Both Sides of the Equation

Sometimes when solving equations, we may encounter variables with coefficients, which we need to remove to isolate the variable and find its value.
Exactly for those cases, and many more, we have the ability to multiply or divide both sides of the equation by the same number to maintain balance and solve for the variable.

With this method, we can multiply or divide both sides of the equation by the same element without thereby altering the overall value of the equation. This means that the final result of the equation will not be affected because we have multiplied or divided both sides by the same element or number.

In order to so we need to follow these two steps:

Identify the Coefficient: Determine if multiplication or division is needed to isolate the variable.
Apply Operation to Both Sides: Multiply or divide by the coefficient’s reciprocal.

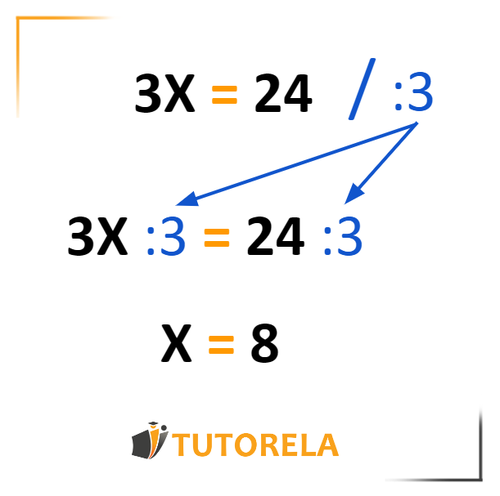
Solving Equations by Multiplying or Dividing Both Sides by the Same Number

It's important to remember that when we multiply or divide both sides of an equation, the equation's balance should remain unchanged. This means we can always reverse the operation to return to the original equation. If reversing leads to a different result, it indicates that an error was made in the calculations.

Detailed explanation

Start practice

Test yourself on solving an equation by multiplication/ division!

Solve for X:

$$ 3x=18 $$

Practice more now

Below, we provide you with some examples where we apply this method.

Example 1

$3X=24$

We solve the equation and find the numerical value of $X$ by dividing both sides of the equation by the number $3$ .

In this way, we neutralize and isolate the $X$ on the left side of the equation, while on the right side we obtain the result of the equation.

$3X=24$ / $:3$

$X=8$

The result of the equation is $8$ .

Example 2

$\frac{X}{2}=5$

We solve the equation and find the numerical value of X by multiplying both sides of the equation by the number 2. This way, we neutralize and isolate X on the left side of the equation, while on the right side we obtain the result of the equation.

$\frac{X}{2}=5$ / $\times2$

$X=10$

The result of the equation is $10$ .

Examples and exercises with solutions for solving equations by multiplying or dividing both sides by the same number

Exercise #1

Solve for X:

$3x=18$

Video Solution

Step-by-Step Solution

We use the formula:

$a\cdot x=b$

$x=\frac{b}{a}$

Note that the coefficient of X is 3.

Therefore, we will divide both sides by 3:

$\frac{3x}{3}=\frac{18}{3}$

Then divide accordingly:

$x=6$

Answer

$6$

Exercise #2

$4=3y$

Video Solution

Step-by-Step Solution

The goal is to solve the equation $4 = 3y$ to find the value of $y$ . To do this, we can follow these steps:

Step 1: Divide both sides of the equation by 3 to isolate $y$ .
Step 2: Simplify the result to solve for $y$ .

Now, let's work through the solution:

Step 1: We start with the equation:

$4 = 3y$

To solve for $y$ , divide both sides by 3:

$y = \frac{4}{3}$

Step 2: Simplify the fraction:

$y = \frac{4}{3} = 1 \frac{1}{3}$

Therefore, the solution to the equation is $y = 1 \frac{1}{3}$ .

This corresponds to choice $y = 1\frac{1}{3}$ in the provided multiple-choice answers.

Answer

$y=1\frac{1}{3}$

Exercise #3

$-7y=-27$

Video Solution

Step-by-Step Solution

To solve the equation $-7y = -27$ , we need to isolate the variable $y$ . We do this by performing the following steps:

Step 1: Divide both sides of the equation by $-7$ to solve for $y$ .

Performing this operation gives us:

-7y \div (-7) = -27 \div (-7)

Simplifying both sides, we have:

y = \frac{27}{7}

To express $\frac{27}{7}$ as a mixed number, we divide 27 by 7:

27 divided by 7 equals 3 with a remainder of 6. Hence, $\frac{27}{7} = 3\frac{6}{7}$ .

Therefore, the solution to the equation is $y = 3\frac{6}{7}$ .

Among the given choices, option 1 matches our result.

Therefore, the solution to the problem is $y = 3\frac{6}{7}$ .

Answer

$3\frac{6}{7}$

Exercise #4

Solve for X:

$5x=25$

Video Solution

Step-by-Step Solution

To solve the equation $5x = 25$ , we will isolate $x$ using division:

Divide both sides of the equation by 5:

\frac{5x}{5} = \frac{25}{5}

After performing the division, we get:

x = 5

Thus, the solution to the equation is $x = 5$ .

Answer

Exercise #5

Solve for X:

$8x=5$

Video Solution

Step-by-Step Solution

To solve the equation $8x = 5$ , follow these steps:

Step 1: Identify the equation $8x = 5$ , where $x$ is the unknown variable.
Step 2: To isolate $x$ , divide both sides of the equation by 8.
This step involves equivalent operations to maintain equality.
Step 3: Perform the division on both sides:
$\frac{8x}{8} = \frac{5}{8}$ .
This simplifies to $x = \frac{5}{8}$ .