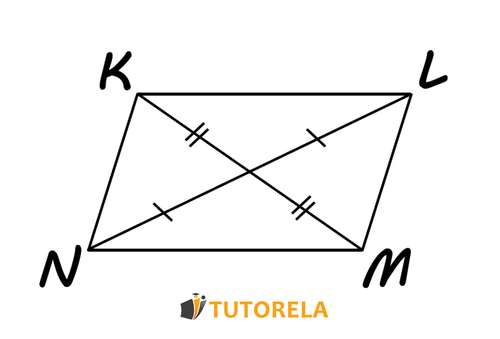
Parallelogram Practice Problems & Exercises with Solutions

Master parallelogram properties, angle calculations, and verification methods with step-by-step practice problems. Perfect for geometry students learning quadrilaterals.

📚What You'll Master in This Parallelogram Practice
  • Identify and apply properties of parallelograms including opposite sides and angles
  • Calculate unknown angles using alternate interior and corresponding angle relationships
  • Verify if quadrilaterals are parallelograms using four different proof methods
  • Solve for missing side lengths and diagonal measurements in parallelograms
  • Apply parallelogram properties to find perimeter and area calculations
  • Master diagonal intersection properties and bisection theorems

Understanding Parallelogram

Complete explanation with examples

Parallelogram

Parallelogram is a four-sided polygon (quadrilateral) where opposite sides are parallel and equal in length. A key feature of parallelograms is that they have two sets of parallel lines, which gives them their name. Examples of parallelograms include squares, rectangles, and rhombuses, which are all specific types of parallelograms with additional unique properties.

Characteristics of the Parallelogram

  • Sides opposite in a quadrilateral: are sides that do not have a common meeting point.
  • Adjacent sides in a quadrilateral: are sides that have a common meeting point.
  • Adjacent angles: are 2 angles that have a common vertex and side.
  • Opposite angles in the quadrilateral are angles that do not have common sides.
  • Diagonal: is a section that connects 2 non-adjacent vertices (and is not a side)

If the data is:

  • ABǁCD AB ǁ CD
  • ADǁBC AD ǁ BC

Then: ABCD ABCD is a parallelogram

Parallelogram

A1 - Parallelogram KLMN

Detailed explanation

Practice Parallelogram

Test your knowledge with 44 quizzes

The parallelogram ABCD is shown below.

What type of angles are indicated in the figure?

AAABBBCCCDDD

Examples with solutions for Parallelogram

Step-by-step solutions included
Exercise #1

Below is a quadrilateral:

Is it possible that it is a parallelogram?

AAABBBCCCDDD711811

Step-by-Step Solution

According to the properties of a parallelogram, any two opposite sides will be equal to each other.

From the data, it can be observed that only one pair of opposite sides are equal and therefore the quadrilateral is not a parallelogram.

Answer:

No

Exercise #2

Below is a quadrilateral:

Is it possible that it is a parallelogram?

AAABBBCCCDDDOOO108810

Step-by-Step Solution

According to the properties of the parallelogram: the diagonals intersect each other.

From the data in the drawing, it follows that diagonal AC and diagonal BD are divided into two equal parts, that is, the diagonals intersect each other:

AO=OC=8 AO=OC=8

DO=OB=10 DO=OB=10

Therefore, the quadrilateral is actually a parallelogram.

Answer:

Yes

Exercise #3

Calculate the area of the parallelogram using the data in the figure:

555888333

Step-by-Step Solution

From the given constraints, it is impossible to confidently compute the area of the parallelogram because of insufficient and unclear relationships between provided figures and the calculations they must produce. Clarity on which numbers correspond to the height and base—as or any definitional angles—is absent.

The correct answer, aligning with acknowledged drawing limitations, is: It is not possible to calculate.

Answer:

It is not possible to calculate.

Video Solution
Exercise #4

Calculate the area of the parallelogram based on the data in the figure:

101010444

Step-by-Step Solution

In this particular problem, despite being given certain measurements, the diagram lacks sufficient clarity to identify which corresponds definitively as the base and which as the perpendicular height of the parallelogram. This insufficiency means that without further context or labeling to avoid assumptions that may lead to error, it is not feasible to calculate the area confidently using the standard formula.

Thus, the answer to the problem is that it is not possible to calculate the area with the provided data.

Answer:

It is not possible to calculate.

Video Solution
Exercise #5

Below is a quadrilateral:

Is it possible that it is a parallelogram?

AAABBBCCCDDD1206012060

Step-by-Step Solution

Let's review the property: a quadrilateral in which two pairs of opposite angles are equal is a parallelogram.

From the data in the drawing, it follows that:

D=B=60 D=B=60

A=C=120 A=C=120

Therefore, the quadrilateral is actually a parallelogram.

Answer:

Yes

Frequently Asked Questions

Everything you need to know about Parallelogram

What are the 4 main properties of a parallelogram?

+
The four main properties are: 1) Opposite sides are parallel and equal, 2) Opposite angles are equal, 3) Diagonals bisect each other, and 4) Adjacent angles are supplementary (add up to 180°).

How do you prove a quadrilateral is a parallelogram?

+
You can prove a quadrilateral is a parallelogram using any of these methods: • Show both pairs of opposite sides are parallel • Prove both pairs of opposite sides are equal • Demonstrate both pairs of opposite angles are equal • Show diagonals bisect each other • Prove one pair of opposite sides is both parallel and equal

What is the difference between corresponding angles and alternate interior angles in parallelograms?

+
Corresponding angles are in the same position at each intersection when a transversal crosses parallel lines. Alternate interior angles are on opposite sides of the transversal and inside the parallel lines, forming a 'Z' pattern. Both are equal when lines are parallel.

How do you find missing angles in a parallelogram?

+
Use these steps: 1) Remember opposite angles are equal, 2) Adjacent angles are supplementary (add to 180°), 3) Apply alternate interior angle theorem for parallel sides, 4) Use the fact that all four angles sum to 360°.

What happens when diagonals of a parallelogram intersect?

+
When diagonals of a parallelogram intersect, they bisect each other at the point of intersection. This means each diagonal is divided into two equal segments, creating four congruent triangles within the parallelogram.

Can a parallelogram have right angles?

+
Yes, a parallelogram can have right angles. When all angles are 90°, it becomes a rectangle. A rectangle is a special type of parallelogram with additional properties like equal diagonals and four right angles.

How do you calculate the perimeter of a parallelogram?

+
The perimeter formula is P = 2(a + b), where 'a' and 'b' are the lengths of adjacent sides. Since opposite sides are equal in a parallelogram, you only need to measure two adjacent sides and double their sum.

What are real-world examples of parallelograms?

+
Common real-world parallelograms include: railway tracks forming parallelograms at intersections, rectangular picture frames, rhombus-shaped tiles, parallelogram-shaped building windows, and the quadrilateral formed by opposite pages in an open book.

More Parallelogram Questions

Click on any question to see the complete solution with step-by-step explanations

Area of a Parallelogram

Trapezoid Problem: Calculate X Using Area=36 and Height=3 Find X in Geometric Figure: Area 21 with Side Length 3 Calculate X in Trapezoid: Area 45 with Height 5 Calculate Parallelogram Area: 6 cm Base × 4.5 cm Height Problem Calculate Parallelogram Area with Base 8 and Height 6: Geometric Problem

Parallelogram

Calculate Parallelogram Area: 90° Perpendicular Height and 40-Unit Side Parallelogram Area Calculation: Using Height CE and Segments 5, 7, and 2 Calculate Parallelogram Area: Rectangle with Perimeter 24 Inside Calculate Parallelogram Area: Circle with Circumference 25.13 and Tangent Points Circle-Parallelogram Tangency Problem: Finding Area of Blue Regions with 25.13 Circumference

Characteristics and Proofs of a Parallelogram

Calculate Parallelogram Side Length DC Using Expression 5x+12 Parallelogram Verification: Comparing Sides x+5 and 2x+9 Parallelogram Properties: When ∢B+∢C=180° in a Quadrilateral Parallelogram Property Investigation: Proving AO = OC in a Quadrilateral Find the Missing Angle X: Converting a Quadrilateral into a Parallelogram with 60° and 120° Angles

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Applying the formula Calculate The Missing Side based on the formula Calculating in two ways Finding Area based off Perimeter and Vice Versa Using additional geometric shapes Using congruence and similarity Using external height Using Pythagoras' theorem Using ratios for calculation Using variables Verifying whether or not the formula is applicable Calculating angle size in a parallelogram Calculating the length of a side in a parallelogram In order for the quadrilateral to be a parallelogram what should the value of the unknown be ? Is this a parallelogram? True / false Using the properties of the perimeter of the parallelogram

More Resources and Links

Explore more resources and links related to Parallelogram
Practice AreaPractice The area of a parallelogram: what is it and how is it calculated?Practice Perimeter of a ParallelogramPractice PerimeterPractice Areas of Polygons for 7th GradePractice How do we calculate the area of complex shapes?Practice How do we calculate the perimeter of polygons?