When students hear the words "compound shapes", they usually feel uncomfortable. Just before you also ask yourself: "Oh, why this again?", you should be aware that there is no real reason. Describing shapes as compound doesn't really make them so. As it turns out calculating areas and perimeters of compound shapes is in fact relatively straightforward.
Area of Rectangle & Complex Shapes Practice Problems
Master rectangle area calculations and decompose complex shapes into familiar rectangles. Practice with step-by-step examples and build confidence solving geometry problems.
📚Practice Calculating Areas of Rectangles and Complex Shapes
- Calculate rectangle area using length × width formula
- Decompose complex shapes into familiar rectangles
- Apply rectangle properties to find missing dimensions
- Add and subtract rectangle areas in composite shapes
- Solve real-world rectangle area word problems
- Master the puzzle method for complex shape areas
Understanding Area of a Rectangle
Complete explanation with examples
How do we calculate the area of complex shapes?
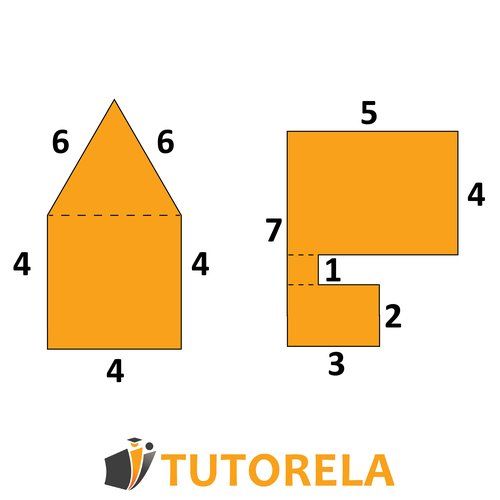
You will be introduced to Complex shapes only after you learn various shapes in geometry. The reason these shapes are complex is due to the fact that they are slightly different from those you've come to know. In each complex shape, additional shapes that you need to identify are hidden. Dividing the complex shape into several different (and familiar) shapes will allow you to answer the question of how to calculate the area of complex shapes.
The trick: extract a familiar shape from within the complex shape
So how do we answer the question of how to calculate the area of complex shapes? First, you need to identify familiar shapes within the complex shape. An example of this: a rectangle. As you know, each shape has properties that you are familiar with, so within the complex shape itself, you can apply the properties of the familiar shape and thus calculate areas and perimeters.
After completing the missing data (according to the properties of each shape, for example: rectangle), you can complete the "puzzle", identify additional data that is revealed to you, and thus calculate the area of the complex shape. When calculating the area of complex shapes, you will often need to perform simple arithmetic operations such as division and addition (mainly for sides in the shape) - all based on the unique properties of each shape.
Practice Area of a Rectangle
Test your knowledge with 126 quizzes
Calculate the area of the triangle using the data in the figure below.
Examples with solutions for Area of a Rectangle
Step-by-step solutions included
Exercise #1
Complete the sentence:
To find the area of a right triangle, one must multiply ________________ by each other and divide by 2.
Step-by-Step Solution
To solve this problem, begin by identifying the elements involved in calculating the area of a right triangle. In a right triangle, the two sides that form the right angle are known as the legs. These legs act as the base and height of the triangle.
The formula for the area of a triangle is given by:
In the case of a right triangle, the base and height are the two legs. Therefore, the process of finding the area involves multiplying the lengths of the two legs together and then dividing the product by 2.
Based on this analysis, the correct way to complete the sentence in the problem is:
To find the area of a right triangle, one must multiply the two legs by each other and divide by 2.
Answer:
the two legs
Exercise #2
Indicate the correct answer
The next quadrilateral is:
Step-by-Step Solution
Initially, let us examine the basic properties of a deltoid (or kite):
A quadrilateral is classified as a deltoid if:
- It has two distinct pairs of adjacent sides that are equal in length.
In the question's image, we observe the following:
- There are lines connecting A to B, B to C, C to D, and D to A, suggesting a typical quadrilateral.
- The shape, given its central symmetry (as it is formed by joining these particular points which extend equal lines), is reminiscent of a symmetric or bilaterally mirrored formation.
- Given the symmetry, it suggests all internal angles are less than 180 degrees, confirming the figure as a convex shape.
From this analysis, the quadrilateral satisfies the characteristic of having pairs of equal adjacent sides which confirms it as a deltoid. The symmetry suggests it is not concave (which occurs when at least one interior angle is greater than 180 degrees).
Therefore, the given quadrilateral, based on its properties and symmetry, is a convex deltoid.
Answer:
Convex deltoid
Video Solution
Exercise #3
Indicate the correct answer
The next quadrilateral is:
Step-by-Step Solution
To solve this problem, let's analyze the given quadrilateral ABCD by examining its geometric properties:
- Step 1: Identifying characteristics of a deltoid
A deltoid, or kite, is a quadrilateral that has two distinct pairs of adjacent sides that are equal. To classify a shape as a deltoid, we need to verify these properties. - Step 2: Examining the quadrilateral ABCD
The deltoid can be either concave or convex. If the shape is concave, it will have an indentation, meaning at least one angle is greater than . A convex deltoid does not have such an indentation. - Step 3: Analyze the sides of ABCD
Looking at the segments from the given points:
- Verify if pairs of adjacent sides are equal.
If we cannot find two equal pairs of adjacent sides, the quadrilateral is not a deltoid. - Step 4: Drawing conclusions
Having analyzed the sides of the quadrilateral, if none of the pairs of adjacent sides conform to the deltoid property as outlined—two pairs of equal adjacent sides—then ABCD is identified as not a deltoid.
Therefore, the correct answer is: Not deltoid.
Answer:
Not deltoid
Video Solution
Exercise #4
Indicate the correct answer
The next quadrilateral is:
Step-by-Step Solution
To solve this problem, let's analyze the quadrilateral depicted:
- Step 1: Analyze the given quadrilateral's shape using its geometric features, noting potential symmetry and side equivalence.
- Step 2: Identify if the quadrilateral fulfills the characteristics of a deltoid, which involve pairs of adjacent sides being equal.
- Step 3: Determine if it is possible to accurately categorize the quadrilateral as a convex or concave deltoid based on the given image and without explicit measurements.
- Step 4: In the absence of direct measurable evidence, consider if categorization is feasible.
Assessing visuals alone can lead to assumptions about equal lengths or angles, but without numerical data, it's challenging to make definitive geometrical claims about sides or symmetry.
Given these limitations, it is reasonable to conclude that we cannot definitively prove whether the quadrilateral is a deltoid (convex or concave) using just the visual representation provided.
Therefore, the solution to the problem is "It is not possible to prove if it is a deltoid or not."
Answer:
It is not possible to prove if it is a deltoid or not
Video Solution
Exercise #5
Indicate the correct answer
The next quadrilateral is:
Step-by-Step Solution
The problem requires determining if a given quadrilateral is a deltoid, and if so, whether it is convex, concave, or indeterminate based on the provided diagram. A deltoid, or kite, is generally defined as a quadrilateral with two pairs of adjacent sides being of equal length. Thus, a visual analysis is essential here as only diagrammatic data is available.
To address this, one must closely analyze the properties of the given quadrilateral in terms of similarity and its symmetry relative to a conventional deltoid structure:
- Typically, you'd look for simultaneous symmetry or patterns indicating two equal-length adjacent pairs of sides.
- After examining the diagram and the naming convention (vertices labelled A, B, C, D), see if it implies any such congruency visually or through label symmetry.
- Lack of distinct clues for equal side pairs or diagonals prevents concluding its specific nature without additional information, especially since no specific length measures or angles are provided.
Given this and under diagram-only conditions, it's not possible to definitively prove that the shape is completely a deltoid (convex or concave). Therefore, without further data, identifying the indicated quadrilateral deltoid nature is beyond determining from the given data itself.
Consequently, the correct answer is: It is not possible to prove if it is a deltoid or not.
Answer:
It is not possible to prove if it is a deltoid or not
Video Solution
Frequently Asked Questions
How do you find the area of a rectangle?
+The area of a rectangle is calculated using the formula: Area = length × width. Simply multiply the length by the width to get the total area in square units.
What is the easiest way to find the area of complex shapes?
+Break down complex shapes into familiar shapes like rectangles. Identify the rectangles within the complex shape, calculate each rectangle's area separately, then add or subtract these areas as needed.
How do you calculate missing dimensions in rectangle problems?
+Use the properties of rectangles: opposite sides are equal. If you know some dimensions, use addition and subtraction to find missing measurements based on the overall shape dimensions.
What are composite shapes in geometry?
+Composite shapes (also called compound shapes) are figures made up of two or more basic shapes combined together. They can be solved by breaking them into rectangles, triangles, or other familiar shapes.
Why do students struggle with complex shape area problems?
+Students often feel overwhelmed because complex shapes look complicated. The key is recognizing that these are just combinations of simple shapes you already know how to solve.
What math operations are needed for rectangle area problems?
+You'll primarily use: 1) Multiplication (length × width), 2) Addition (combining areas), 3) Subtraction (removing overlapping areas), 4) Basic arithmetic to find missing dimensions.
How do you solve L-shaped area problems?
+Divide the L-shape into two rectangles. Calculate each rectangle's area using length × width, then add the two areas together for the total area of the L-shaped figure.
What are common mistakes when calculating rectangle areas?
+Common errors include: mixing up length and width, forgetting to include units, adding dimensions instead of multiplying them, and not properly identifying rectangles within complex shapes.