Perimeter of a Parallelogram Practice Problems & Exercises

Understanding Perimeter of a Parallelogram

Complete explanation with examples

The formula to calculate the perimeter of a parallelogram

You have probably already realized that it is not necessary to calculate all the edge lengths to find the perimeter.

Let's look at the parallelogram $ABCD$ :

The equal edges are marked with the letters $a$ and $b$ . Let's note the perimeter of the parallelogram:
$P=a+a+b+b=2a+2B=2\left(a+b\right)$

Now let's do it in a clear way.

The formula to calculate the perimeter of a parallelogram is:
$P=2a+2b$

or
$P=2(a+b)$

There is no difference between both formulas, we can use whichever we want.

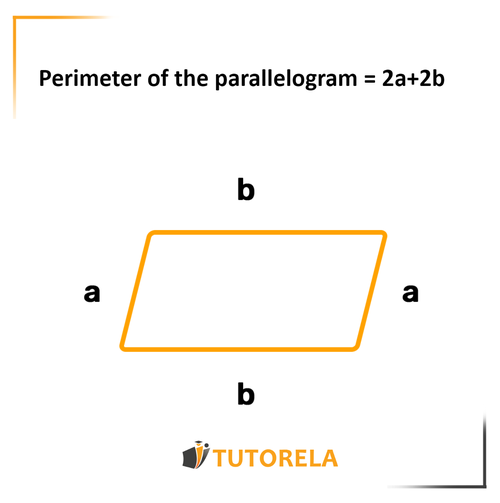
The perimeter of the parallelogram is equal to the sum of its four edges (or sides). As we know, in a parallelogram there are two pairs of opposite edges of equal length, therefore, knowing the length of two adjacent sides is enough to calculate the perimeter of the figure.

For example, if we observe the parallelogram $ABCD$ , given the length of its sides in cm:

As we have mentioned, the perimeter is the sum of the length of its sides. Consequently, we will note:

$P=3+4+3+4=14$

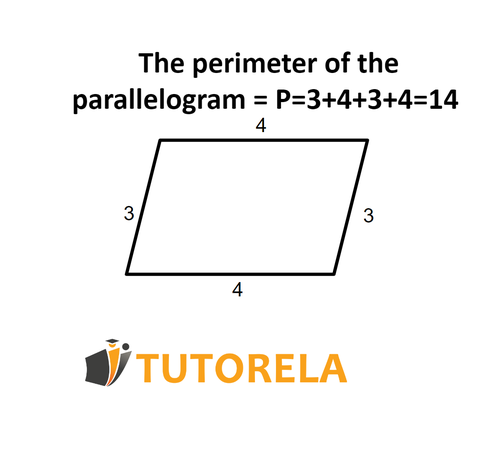
Solution: The perimeter of the parallelogram is $14cm$ .

Detailed explanation

Practice Perimeter of a Parallelogram

Test your knowledge with 19 quizzes

Given the parallelogram:

Calculate the perimeter of the parallelogram.

Examples with solutions for Perimeter of a Parallelogram

Step-by-step solutions included

Exercise #1

Calculate the perimeter of the given parallelogram:

Step-by-Step Solution

As is true for a parallelogram every pair of opposite sides are equal:

$AB=CD=6,AC=BD=4$

The perimeter of the parallelogram is equal to the sum of all sides together:

$4+4+6+6=8+12=20$

Answer:

20

Video Solution

Exercise #2

Given the parallelogram:

Calculate the perimeter of the parallelogram.

Step-by-Step Solution

To solve this problem, let's follow these steps:

Step 1: Identify the lengths of the adjacent sides of the parallelogram.
Step 2: Use the formula for the perimeter of a parallelogram, $P = 2(a + b)$ .
Step 3: Plug in the known values and calculate the perimeter.

Now, let's work through each step:

Step 1: From the diagram, we have two adjacent sides of the parallelogram: $a = 8$ units and $b = 3$ units.

Step 2: The formula for the perimeter of a parallelogram is given by $P = 2(a + b)$ .

Step 3: Substitute the values for $a$ and $b$ into the formula:

$P = 2(8 + 3) = 2 \times 11 = 22$ .

Therefore, the perimeter of the parallelogram is $22$ .

Answer:

22

Video Solution

Exercise #3

Given the parallelogram:

Calculate the perimeter of the parallelogram.

Step-by-Step Solution

To solve the problem of calculating the perimeter of the parallelogram, follow these steps:

Identify the given side lengths: $AB = 5$ and $AC = 4$ .
Acknowledge that in a parallelogram, opposite sides are equal, so $AB = CD = 5$ and $AC = BD = 4$ .
Apply the perimeter formula for a parallelogram: $P = 2 \times ( \text{Base} + \text{Side} )$ .

Plug the known side lengths into the formula:
$P = 2 \times (AB + AC) = 2 \times (5 + 4) = 2 \times 9 = 18$

Thus, the perimeter of the parallelogram is $18$ .

Answer:

18

Video Solution

Exercise #4

Calculate the perimeter of the given parallelogram.

Step-by-Step Solution

As is true for a parallelogram each pair of opposite sides are equal and parallel,

Therefore it is possible to argue that:

$AC=BD=7$

$AB=CD=10$

Now we can calculate the perimeter of the parallelogram by adding together all of its sides:

$10+10+7+7=20+14=34$

Answer:

34

Video Solution

Exercise #5

Given the parallelogram:

Calculate the perimeter of the parallelogram.

Step-by-Step Solution

To solve this problem, we'll follow these steps:

Step 1: Identify the given side lengths of the parallelogram.
Step 2: Apply the perimeter formula for a parallelogram.
Step 3: Perform the calculation with the identified side lengths.

Now, let's work through each step:
Step 1: The problem gives us the side lengths of the parallelogram as $AB = 5$ and $BC = 2$ . Since opposite sides are equal in a parallelogram, we have $AB = CD = 5$ and $BC = DA = 2$ .
Step 2: We'll use the formula for the perimeter of a parallelogram: $P = 2(a + b)$ .
Step 3: Substituting the values, we have:

P = 2(5 + 2) = 2 \times 7 = 14

Therefore, the perimeter of the parallelogram is $\boxed{14}$ .

The correct multiple-choice answer is 14, which corresponds to choice number 2.

Answer:

14

Video Solution

Frequently Asked Questions

Everything you need to know about Perimeter of a Parallelogram

What is the formula for the perimeter of a parallelogram?

+

The perimeter of a parallelogram is P = 2(a + b) or P = 2a + 2b, where 'a' and 'b' are the lengths of two adjacent sides. Since opposite sides in a parallelogram are equal, you only need to know two adjacent side lengths to calculate the perimeter.

How do you find the perimeter of a parallelogram with sides 5cm and 8cm?

+

Using the formula P = 2(a + b), substitute the values: P = 2(5 + 8) = 2(13) = 26cm. You can also calculate it as P = 5 + 5 + 8 + 8 = 26cm since opposite sides are equal in a parallelogram.

How do you find a missing side length when given the perimeter?

+

Use the perimeter formula and solve for the unknown side. For example, if P = 20cm and one side is 6cm, then 20 = 2(6 + b), so 20 = 12 + 2b, therefore 2b = 8, and b = 4cm.

What property of parallelograms helps calculate perimeter easily?

+

The key property is that opposite sides of a parallelogram are equal in length. This means you only need to measure two adjacent sides instead of all four sides to calculate the perimeter.

Can you solve parallelogram perimeter problems with variables?

+

Yes, you can solve algebraic problems involving parallelogram perimeter. Steps include: 1) Write the perimeter formula P = 2(a + b), 2) Substitute known values and variables, 3) Solve the resulting equation for the unknown variable, 4) Check your answer by substituting back into the original equation.

What are common mistakes when finding parallelogram perimeter?

+

Common errors include: adding all four sides instead of using the formula when only two sides are given, forgetting that opposite sides are equal, mixing up which sides are adjacent versus opposite, and arithmetic errors when solving algebraic equations.

How is parallelogram perimeter different from rectangle perimeter?

+

Both use the same formula P = 2(a + b) since rectangles are special types of parallelograms. However, rectangles have right angles while general parallelograms have opposite angles equal but not necessarily 90 degrees.

What units are typically used for parallelogram perimeter problems?

+

Perimeter is measured in linear units such as: centimeters (cm), meters (m), inches (in), feet (ft), or any other length unit. The answer will always be in the same units as the given side lengths, representing the total distance around the parallelogram.

Continue Your Math Journey

Master Perimeter of a Parallelogram first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Perimeter How do we calculate the perimeter of polygons?

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Applying the formula Calculate The Missing Side based on the formula Finding Area based off Perimeter and Vice Versa Using additional geometric shapes Using the properties of the perimeter of the parallelogram Using variables

Perimeter of a Parallelogram Practice Problems & Exercises

Understanding Perimeter of a Parallelogram

Practice Perimeter of a Parallelogram

Examples with solutions for Perimeter of a Parallelogram

Frequently Asked Questions

What is the formula for the perimeter of a parallelogram?

How do you find the perimeter of a parallelogram with sides 5cm and 8cm?

How do you find a missing side length when given the perimeter?

What property of parallelograms helps calculate perimeter easily?

Can you solve parallelogram perimeter problems with variables?

What are common mistakes when finding parallelogram perimeter?

How is parallelogram perimeter different from rectangle perimeter?

What units are typically used for parallelogram perimeter problems?

More Perimeter of a Parallelogram Questions