Which statement is true according to the graph below? 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 8 8 8 0 0 0

The graph intersects the x axis at the point $$ (4,0) $$.

The graph intersects the y axis at the point $$ (0,4) $$.

The graph passes through $$ (5,3) $$.

Which statement best describes the graph below? x y

The graph represents an ascending function.

The graph represents a decreasing function.

The graph represents a constant function.

Does the first graph of the function pass through the origin of the axes? 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 –5 –5 –5 –4 –4 –4 –3 –3 –3 –2 –2 –2 –1 –1 –1 1 1 1 2 2 2 3 3 3 0 0 0 x y II I

Yes, it goes through $$ (0,0) $$

No, it passes through $$ (3,2) $$

No, the second graph is cut off at point $$ (1,2) $$

Which expressions represent linear functions and parallel lines?

$$ y=2(x^2+1) $$ $$ y=2x^2+2 $$

Which of the following describes linear functions and parallel lines?

$$ y=-4(x+1) $$ $$ y=8x-12(x+1) $$

Which of the following represent linear functions and parallel lines?

$$ y=\frac{1}{2}x+10 $$ $$ y=\frac{1}{2}(x+2) $$

Graphs of Direct Proportionality Functions

The graphical representation of a function that represents direct proportionality is actually the ability to express an algebraic expression through a graph.

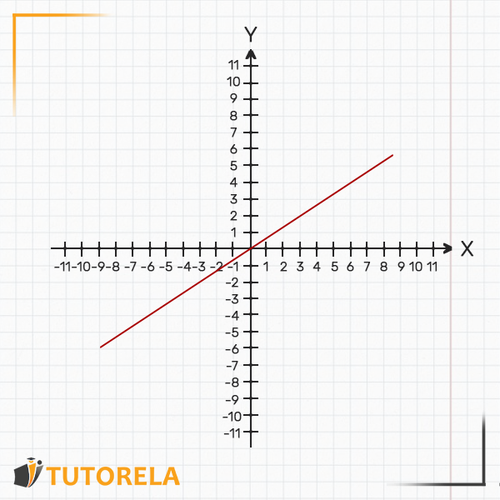
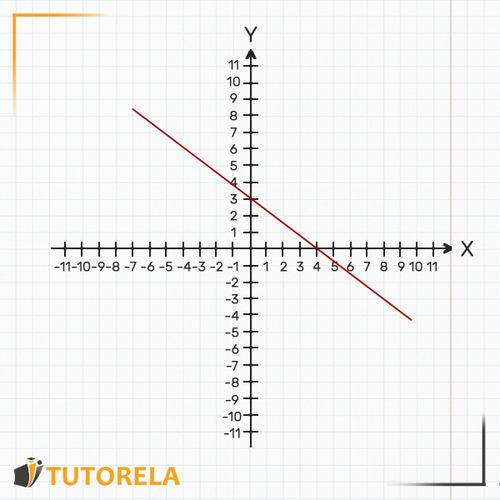
As it is a direct proportionality, the graph will be of a straight line.

A function that represents direct proportionality is a linear function of the family $y=ax+b$ .

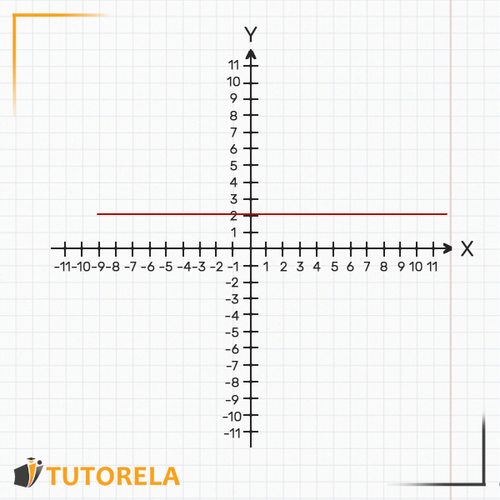
The graphical representation of this function is a straight line that is ascending, descending, or parallel to the $X$ axis but never parallel to the $Y$ axis.

Note: we observe the line from left to right.

We can now recognize in the equation of the line what the graphical representation of each function looks like:

(only when the equation is explicit $Y$ is isolated on one side and its coefficient is $1$ )

A - Graphs of Direct Proportionality Functions

Detailed explanation

Start practice

Test yourself on graphical representation!

Which statement is true according to the graph below?

Practice more now

A -> the slope of the line

When $a > 0$ is positive: the line is ascending

1- When a is positive the line is ascending

When $a < 0$ is negative: the line is descending

2 -When a is negative the line is descending

When $a = 0$ : the line is parallel to the $X$ axis

B -> the point of intersection with the Y-axis

$b$ the y-intercept $Y$

$b$ indicates at which point the line crosses the $Y$ axis.

If $b$ has a positive coefficient, the line will intersect the positive part of the $Y$ axis at the point $b$ .

If b has a negative coefficient, the line will intersect the negative part of the $Y$ axis at the point $b$ .

If $b=0$ , the line will cross the $Y$ axis at the origin where $Y=0$ .

To know exactly what the graph of the line's equation looks like, we will have to examine both parameters at the same time, both a and $b$ .

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Which statement best describes the graph below?

Question 2

Choose the correct answer

$$

Question 3

Does the first graph of the function pass through the origin of the axes?

Examples of Graphical Representation of a Linear Function

Example 1 (use of the graph)

$y=5x-4$
We will examine the linear equation.

$a=5$ The slope is positive, the line ascends
$b=-4$ The line crosses the $Y$ axis at the point where $Y=-4$

We will plot the graph based on the data:

Keep in mind that this is just a sketch.

If you want to draw the graph accurately, you can construct a table of values for $X$ and $Y$ and find out the points that form the line.

Example 2 (using the table)

The function $y=2X$ represents a direct proportionality between the values of $X$ and $Y$ . That is, for each value of $X$ that we input, the value of $Y$ will be double.

We will replace three different values and obtain:

for each value of X that we input, the value of Y will be double

Now let's plot the three points on the coordinate system and connect them. This is actually the graph of the function for $y=2X$ .

Examples and Exercises with Solutions on Graphical Representation of a Function Representing Direct Proportionality

Exercise #1

Which statement is true according to the graph below?

Video Solution

Step-by-Step Solution

If we plot all the points, we'll notice that point $(3,5)$ is the correct one, because:

$x=3,y=5$

And they intersect exactly on the line where the graph passes.

Answer

The graph passes through $(3,5)$ .

Exercise #2

At which point does the graph of the first function (I) intersect the graph of the second function (II)?

Video Solution

Step-by-Step Solution

Let's pay attention to the point where the lines intersect. We'll mark it.

We'll find that:

$X=4,Y=2$

Therefore, the point is:

$(4,2)$

Answer

$(4,2)$

Exercise #3

At what point does the graph intersect the x axis?

Video Solution

Step-by-Step Solution

Note that the line intersects only the Y-axis. In other words, it does not touch the X-axis at all.

Therefore, the answer is D.

Answer

Does not cut the axis x

Exercise #4

A straight line has a slope of 6y and passes through the points $(6,41)$ .

Which function corresponds to the line described?

Video Solution

Step-by-Step Solution

To solve the exercise, we will start by inserting the available data into the equation of the line:
y = mx + b
41 = 6*6 + b
41 = 36 +b
41-36 = b
5 = b

Now we have the data for the equation of the straight line:

y = 6x + 5
But it still does not match any of the given options.

Keep in mind that a common factor can be excluded:
y = 2(3x + 2.5)

Answer

$y=2(3x+2\frac{1}{2})$

Exercise #5

Does the first graph of the function pass through the origin of the axes?

Video Solution

Answer

No, it passes through $(3,1)$

Do you know what the answer is?

Question 1

At which point does the graph of the first function (I) intersect the graph of the second function (II)?

Question 2

At what point does the graph intersect the yaxis?

Question 3

At what point does the graph intersect the x axis?

Start practice