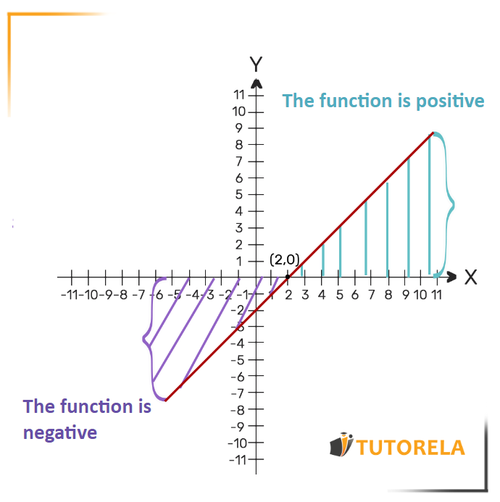
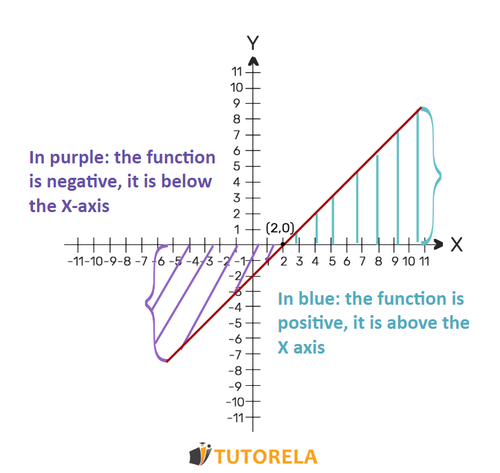
Positivity and Negativity of a Linear Function
The function is positive when it is above the axis when
The function is negative when it is below the axis as
When we are asked what the domains of positivity of the function are, we are actually being asked in which values of the function is positive: when it is above the axis.
In which values of does the function obtain positive values?
When we are asked what the domain of negativity of the function is, we are actually being asked in which values of the function is negative: when it is below the axis.
In which values of does the function obtain negative values?