Solving a System of Linear Equations with Two Variables Using Algebraic Method

In the first stage:

Let's isolate one variable in an equation of our choice.

In the second stage:

Let's substitute the isolated variable into the second equation in the system to find the value of one variable.

In the third stage:

Let's substitute the value of the unknown we found in a certain equation in order to find the value of the second unknown.

To better understand the substitution method, let's look at an example.

We promise you that after the example and with a little practice, you'll be able to use the substitution method without any problem.

Let's take the following system of equations as an example:

$3y-x=4$

$2x-3y=7$

In this system, there are two linear equations with two unknowns - $X$ and $Y$.

According to the first step, we need to isolate one variable in one equation that we choose.

Which equation should we choose and which variable?

The truth is that it doesn't matter which equation you choose and which variable you choose to isolate, as long as you do it correctly, you'll reach the right answer.

To avoid as many mistakes and confusion as possible,

Let's choose an equation where one of the variables has no coefficient in front of it or has a simple coefficient (like 1 or -1)

This way it will be easier for us to extract and isolate it.

In our example in the first equation, the coefficient of $X$ is -1.

Therefore, we will choose this equation and isolate $X$.

After moving terms and isolating we get:

$x=3y-4$

Remember, moving terms between sides and isolating variables do not change the equation itself but only its appearance, therefore the isolated equation is equivalent to the original equation.

Let's move on to the second stage:

Let's substitute the isolated variable – $X$ into the second equation in the system.

Currently, $X$ has no numerical value, but it has an expression equal to it which is $3y-4$.

Let's take the second equation in the system-
$2x-3y=7$

and we'll substitute $X$ with $3y-4$ as follows:

$2\cdot3y-4-3y=7$

Pay attention!!

It is very important to add parentheses in the expression where you substituted the $X$ to avoid mistakes and confusion.

In this example, the coefficient 2 acts on the entire expression, and if we had forgotten the parentheses, we would have gotten the impression that we need to multiply the 2 only by 3Y.

Therefore, do yourself a favor and don't forget parentheses when substituting an expression as a variable.

What we did was essentially replace $X$ with an expression that has only $Y$.

Thus, we got an equation with one variable that is easy for us to solve.

Now let's continue solving the equation and find $Y$:

Let's open the parentheses, combine like terms, move terms between sides, and isolate $Y$-

$6y-8-3y=7$

$3y=15$

$y=5$

Wait, we're not done yet. To fully solve the system, we need to find both unknowns.

Let's move on to the third stage:

Now, we know that $y=5$.

All we need to do to find X is to simply substitute the $Y$ we found, in our example 5, into one of the equations.

No matter which equation we choose, we will get the same $X$.

We recommend you to immediately approach the equation where we isolated $X$, substitute $y=5$ and find the value of $X$ in the fastest way possible.

Let's go back to the isolated equation of $X$ :

$x=3y-4$

We found $Y$, it is no longer unknown, therefore we substitute: $y=5$

and we get:

$x=3*5-4$

$x=11$

And that's it, we're done. We found the pair of values $X$ and $Y$ that satisfy both equations in the system.

Our tip:

We won't always have equations without coefficients before the variable or simple coefficients. What we need to consider in order to reach isolation in the easiest way is to avoid isolation that will create fractions in the equation.

For example, in the system of equations:

$4x+2y=10$

$3x-5y=4$

Let's ask ourselves which equation would be easier for me to isolate.

Looking at the coefficients, we can notice that in the first equation, we can divide the coefficient 2 by 4 and by 10 evenly, while if we try to isolate one variable in the second equation, we'll get an equation with fractions.

Therefore in this example, if we want to use the substitution method, we will prefer to isolate $Y$ in the first equation.

Think of these questions as a puzzle where you need to discover its parts.
After discovering the first unknown, the path to discovering the second unknown is quick and easy.
The secret to success in exercises like these is practice, practice, and more practice.
If you practice, the substitution method will be well ingrained in your mind and you'll be able to use it naturally.

Remember when we said there are two groups for solving algebraically?

The second method for solving a system of equations with two variables algebraically is the coefficients comparison method.
Solving a system of two linear equations with two variables using the coefficients comparison method
There's a reason why this method is called the coefficients comparison method.
All we need to do is compare the coefficients and sometimes we won't even need to isolate any variable.

How do we do this?

Let's take the following system of equations as an example:

$5X+6Y=7$

$5X+4Y=13$

Look at the two equations before you and notice that the coefficients of the variable $X$ are identical in both.

In both equations, the coefficient of the unknown $X$ is 5.

When there are identical coefficients for a specific variable in both equations, we can subtract one equation from the other.

The simplifier added the minus sign as follows:

Now, subtract each variable separately and get:

$0+2y=-6$

You didn't understand how we subtracted the equations?

Look at the following illustration:

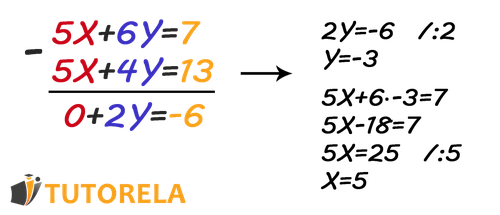
Make sure to arrange the equations so that each variable is aligned one above the other accordingly.

$X$ over $X$

$Y$ over $Y$

Number over number

Actually we got the equation $2y=-6$

Let's isolate $Y$ and get $y=-3$

Now we will find the unknown $X$.

Let's substitute $y=-3$ in one of the equations and we'll get $x=5$.

No matter which equation we choose to substitute $y=-3$ into, we will get the same result.

When you identify identical coefficients of the same variable in two equations, it is highly recommended to use the method of comparing coefficients.

When else should we use the method of comparing coefficients?

Sometimes the coefficients will not be identical in both equations.

Even in cases where the coefficients are opposite, meaning minus and plus, it is highly beneficial for us to use the method of comparing coefficients. Before we can use it, we need to better understand the meaning of this method.

Let's take the following system of equations as an example:

Example of solving by comparing coefficients when the coefficients are opposite in one of the variables:

$5X+6Y=7$

$-5X+4Y=13$

In fact, this system is very similar to the system of equations given in the previous example.

The keen-eyed will notice that the coefficients of $X$ in this system of equations are not identical. They are similar, 5 and -5, but they are not identical.
If we subtract the equations as we did in the previous example, we'll get a new equation with two variables and essentially haven't made any progress.
The purpose of comparing coefficients is to reach a situation where one variable is eliminated, completely disappears.

So what can we do to eliminate the variable $X$ in this system?

Add the equations instead of subtracting them!
If we add the equations, we'll cancel out the X coefficient and remain with only one variable.
Let's see this in the example:

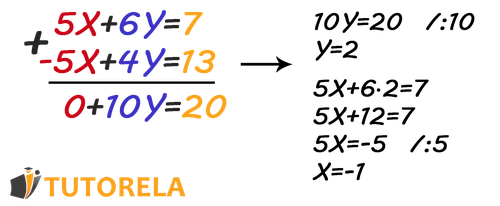
We combined the equations in the same way as we did in the first example - factor over factor respectively and we got:

$10Y=20$

Let's isolate $Y$ and get $y=2$.

Have we finished solving the system of equations? No and no!|
To solve the system of equations and get a complete solution, we must not forget to find both $X$ and $Y$.

Substitute $y=2$ that you found in any equation you choose from the two equations in the system and find the value of $X$.

Let's substitute $y=2$ into the first equation and we get:

$5x+6\cdot2=7$
$5x=-5$
$x=-1$

The solution to the system of equations is $x=-1, y=2$

Want to make sure you got it right?

Substitute the values you found into both equations and check if the equation holds.

What happens when we have a system of equations with coefficients that are neither identical nor opposite, and we are asked to solve the system using the method of equating coefficients? Let's look at an example.

The following system of equations is given -

$3X-2Y=11$

$6x+5y=4$

The coefficients of none of the variables are identical or opposite.

Therefore, we need to perform a preliminary step before adding and subtracting the equations.
The preliminary step is - making the coefficient of one variable identical or opposite in both equations.
If we perform a certain mathematical operation like division or multiplication on both sides, the equation might look different but will be equivalent to the original equation, and this is exactly the key to solving these types of questions.

Look at the system of equations above.

Focus on the coefficients and note the following fact -

If we look at the coefficients of $X$ we'll notice that with a simple operation we can turn a, 3 into 6 if we just multiply it by 2.

What about the coefficients of $Y$? Here we'll get a bit more complicated because we'll need to perform mathematical operations on both equations.

Therefore, we will decide that we want to make the coefficient of the first equation also 6 because all we need to do is a simple mathematical operation - multiply both sides of the first equation only by 2.

Let's see it through the example-

$3X-2Y=11$

$6x+5y=4$

We get:

$2\cdot3x-2y=22$

$6x+5y=4$

Remember! In order to get an equivalent equation, you must multiply both sides of the equation.
If on one side there is an expression like in our example, don't forget to put it in parentheses and multiply the entire parentheses by the factor we want to multiply by.
Let's continue solving the parentheses and we'll get:

$6x-4y=22$

This is the new equivalent equation.
We managed to make the coefficients of $X$ identical in both equations.
Now, we'll implement the solving method we learned for comparing coefficients when the coefficients are identical in one of the variables.
We'll write the equations one below the other in the correct order, subtract the equations, find one variable, substitute it in one of the equations, and get the second variable.

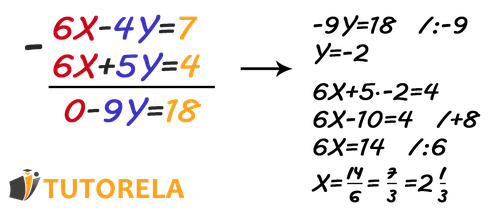
We won't forget to substitute $Y$ into one of the original equations to find $X$ and we'll get that $x=73$.

Actually, when you receive a system of linear equations with two variables and want to use the coefficients comparison method, first look at the equations and check which case the system matches.

Whether the coefficients are identical in one variable, opposite in one variable, or completely different, and thus you will operate correctly and efficiently.

Sometimes we may encounter a system of equations that has no solution or has infinite solutions.

If we have a system of two equations where the coefficients of both variables are identical in both equations, meaning the coefficient of $X$ is identical in both equations and the coefficient of $Y$ is identical in both equations but the constant term is not identical, we will get an expression of:

$0=any~number~that~is~not~zero$

This expression is false! 0 cannot equal any number other than 0, so we'll say that this system of equations has no solution.

On the other hand, if the coefficients are identical in both equations with two unknowns and the constant term is also identical (two completely identical equations), we can immediately determine that this system has infinite solutions.

Why? Because no matter which $Y$ and $X$ we choose, since these are two completely identical equations, we'll get the same expression.

Another way to understand this using the coefficient method is to subtract between the identical equations and get $0=0$. A true expression.
Great! Now you know how to solve a system of linear equations with two variables using an algebraic method.
Wait... but what happens when you're not given the system and you need to build it from a word problem?

Good question.

Sometimes, when they want us to think a bit more and deduce the data ourselves, we won't be given a system of equations but rather a word problem from which we'll need to determine the relevant equations.

In general, we need to understand the conditions in the question and create the correct equations through them.

Let's see it through an example.

Here's a question-

What is the price of pants and the price of a shirt if it is known that the price of pants is twice the price of a shirt and the price of 5 pairs of pants is 22$ more than the price of 8 shirts?

Okay.
You might be looking at this question and wondering how you can turn it into a system of equations with two variables.
Don't worry, it's not that complicated. You just need to focus and read the question carefully.

In the initial stage, we will read the question without writing down the data.

From the first reading, we understand that there are two unknowns to discover - the price of pants and the price of a shirt.
We are given information about these prices and are presented with conditions that they must meet, for example - the price of pants is double the price of a shirt.

In the second stage - let's decide to call our unknowns with the letters $X$ and $Y$.

Randomly, let's mark and write:

$X$- price of a shirt

$Y$- price of pants

The third step is to convert the data written in words into relevant equations.

How will we do this?
Let's start reading the question again and encounter the first condition - the price of pants is double the price of a shirt.
This means that in order for the price of pants to be equal to the price of a shirt, we need to multiply the shirt's price by 2.
We know this might sound a bit confusing, but if you focus you'll understand that since the pants' price is double the shirt's price, in order to compare between them we'll need to multiply the shirt's price in the following way:

$y=2x$

Note that we previously marked $X$ as the price of the shirt and $Y$ as the price of the pants.

This is the first equation in our system of equations.
Now we'll continue reading the question and encounter the second condition - the price of 5 pants is 22$ more than the price of 8 shirts.
In other words, to create an equation - to compare between the price of a shirt and pants, we'll need to perform different operations.
This condition is slightly more complex than the first one, but once you understand the technique, it will come to you very quickly.

The price of $5$ pairs of pants, which is $5Y$, is greater by $22$ than the price of $8$ shirts, which is $8X$.

In fact, we need to add $22$ to the price of eight shirts – $8X$ to equal the price of $5$ pants – $5Y$.

Let's express this in an equation:

$5y=8x+22$

Another way to understand this condition is to understand that the difference between the price of 5 pairs of pants and the price of 8 shirts is 22, and then we get an equation equivalent to the equation we found, just in a different order:

$5y-8x=22$

Now, we also have the second equation and we can put them into a system of equations:

$y=2x$

$5y-8x=22$

We can choose whichever method we want - comparing coefficients or substitution to find the two unknowns.

In this case, when $Y$ is already isolated, we would recommend simply substituting it into the second equation, finding the value of $X$, and then not forgetting to go back and find the value of $Y$.

Remember what they asked you in the question - what is the price of pants and what is the price of a shirt.

In this example:

$5\cdot2x=8x+22$

$10x=8x+22$

$2x=22$

$x=11$

We marked $X$ as the price of the shirt, therefore the shirt price is 11$.

Now, let's calculate the price of the pants:

Let's substitute $x=11$

In the simplest equation:

$y=2x$

And we get:

$y=2x$

In other words, the price of the pants is 22$.

The key to success in solving these types of questions is to read the question several times and understand exactly what it's trying to tell us.

Work with the steps we wrote for you above, practice additional questions, encounter different cases, and you can be confident that you master the material wonderfully.