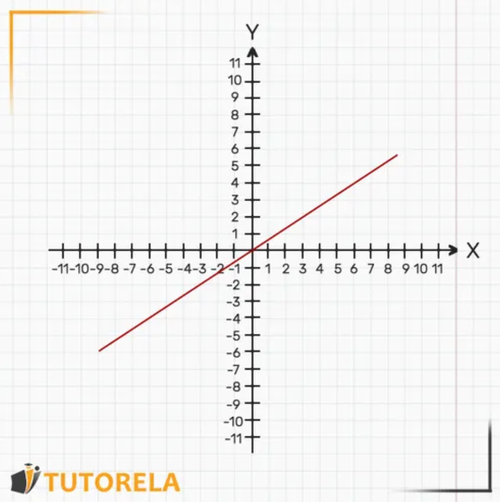
The linear function actually represents a graph of a straight line that has a point of intersection with the vertical axis.
represents the slope.
When is positive, the slope is positive: the line goes upwards.
When is negative, the slope is negative: the line goes downwards.
When , the slope is zero: the line is parallel to the axis.
represents the point where the line intersects the axis.
If , then the line will pass through the origin of the coordinates, that is, the point
For the function in front of you, the slope is?
If we are given a point, we can place it into the equation of a line to see if the equation holds true.
If we are given just one part of the point: or , we will put the given value into the equation correctly and find the second part of the point.
If we want a precise drawing, we'll build a table of values with or fewer values.
We replace each time and obtain the value of .
We consider the slope of the function to be increasing, decreasing, or equal to , and then we graph it.
For the function in front of you, the slope is?
For the function in front of you, the slope is?
For the function in front of you, the slope is?
To calculate the slope, we can use a formula that finds it using two given points that the line passes through:
We are given a linear function .
We are asked to interpret the values and and plot the graph of the function.
First, it appears that , meaning represents the slope of the line (or function).
means that the line intersects the vertical axis (the y-axis) at .
To plot the graph, all we need are points.
We substitute values and obtain:
Now we will mark the two points on the coordinate system and connect them.
Looking at the graph, we can confirm that the plot intersects the y-axis at the value of .
Which best describes the function below?
Remember that the rate of change equals the slope.
In this function:
Therefore, the function is decreasing.
The function is decreasing.
Given the linear function:
What is the rate of change of the function?
Let's remember that the rate of change equals the slope.
In this case, the slope is:
Calculate the slope of the line that passes through the points .
Remember the formula for calculating a slope using points:
Now, replace the data in the formula with our own:
-2
What is the slope of a straight line that passes through the points ?
To solve the problem, remember the formula to find the slope using two points
Now, we replace the given points in the calculation:
Choose the correct answer for the function.
Let's start with option A
In a linear function, to check if the functions are parallel, you must verify if their slope is the same.
y = ax+b
The slope is a
In the original formula:
y = -x+1
The slope is 1
In option A there is no a at all, which means it equals 1, which means the slope is not the same and the option is incorrect.
Option B:
To check if the function passes through the points, we will try to place them in the function:
-1 = -(-2)+1
-1 = 2+1
-1 = 3
The points do not match, and therefore the function does not pass through this point.
Option C:
We rearrange the function, in a way that is more convenient:
y = -1-x
y = -x-1
You can see that the slope in the function is the same as we found for the original function (-1), so this is the solution!
Option D:
When the slope is negative, the function is decreasing, as the slope is -1, the function is negative and this answer is incorrect.
The graph is parallel to the graph of function
For the function in front of you, the slope is?
For the function in front of you, the slope is?
For the function in front of you, the slope is?
