Graphical Representation of a Function - Examples, Exercises and Solutions

Understanding Graphical Representation of a Function

Complete explanation with examples

As we learned in an article on functions, the standard "correspondence rule" is a connection between a dependent variable (Y) (Y) and an independent variable (X) (X) .

By means of a graph or drawing, which gives a visual aspect to the concept of the function. From the graph it is possible to understand whether it is a linear function (straight line), a quadratic function (parabola) and more.

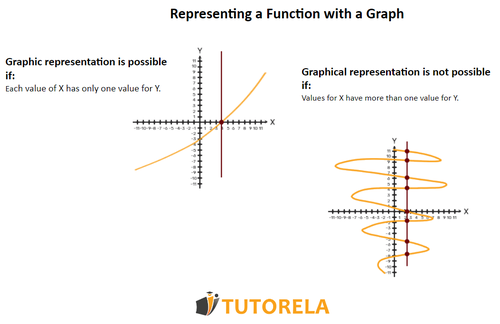
Remember that when it comes to a graphical representation of a function, each point in the domain X X will always have only one point within the range Y Y . Therefore, not every drawing is a graphical representation of a function. Here is an example.

A1 - Graphical representation of a function

Detailed explanation

Practice Graphical Representation of a Function

Test your knowledge with 12 quizzes

Which of the following equations corresponds to the function represented in the graph?

–8–8–8–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777888–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444000

Examples with solutions for Graphical Representation of a Function

Step-by-step solutions included
Exercise #1

Determine whether the following table represents a function

XY-1015811

Step-by-Step Solution

It is important to remember that a constant function describes a situation where as the X value increases, the function value (Y) remains constant.

In the table, we can observe that there is a constant change in X values, meaning an increase of 1, and a constant change in Y values, meaning an increase of 3

Therefore, according to the rule, the table describes a function.

Answer:

Yes

Video Solution
Exercise #2

Determine whether the data in the following table represent a constant function

XY012348

Step-by-Step Solution

It is important to remember that a constant function describes a situation where as the X value increases, the function value (Y) remains constant.

In the table, we can observe that there is a constant change in X values, meaning an increase of 1, and a non-constant change in Y values - sometimes increasing by 1 and sometimes by 4

Therefore, according to the rule, the table does not describe a function

Answer:

No

Video Solution
Exercise #3

Determine whether the following table represents a constant function:

XY02468-3-3-3-3-3

Step-by-Step Solution

It is important to remember that a constant function describes a situation where, as the X value increases, the Y value remains constant.

In the table, we can see that there is a constant change in the X values, specifically an increase of 2, while the Y value remains constant.

Therefore, the table does indeed describe a constant function.

Answer:

Yes, it does

Video Solution
Exercise #4

Is the given graph a function?

–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777–4–4–4–3–3–3–2–2–2–1–1–1111222333000

Step-by-Step Solution

It is important to remember that a function is an equation that assigns to each element in domain X one and only one element in range Y

Let's note that in the graph:

f(0)=2,f(0)=−2 f(0)=2,f(0)=-2

In other words, there are two values for the same number.

Therefore, the graph is not a function.

Answer:

No

Video Solution
Exercise #5

Determine whether the given graph is a function?

–7–7–7–6–6–6–5–5–5–4–4–4–3–3–3–2–2–2–1–1–1111222333444555666777–4–4–4–3–3–3–2–2–2–1–1–1111222333000

Step-by-Step Solution

It is important to remember that a function is an equation that assigns to each element in domain X one and only one element in range Y

We should note that for every X value found on the graph, there is one and only one corresponding Y value.

Therefore, the graph is indeed a function.

Answer:

Yes

Video Solution

More Graphical Representation of a Function Questions

Click on any question to see the complete solution with step-by-step explanations

Representations of Functions

Match the Function Equation: Analyzing X-Y Values from -3 to 5 Graph to Equation Puzzle: Identify the Matching Function Decipher the Graph's Story: Which Equation Represents This Function? Equation Alignment for Table Mapping of X and Y Identify the Correct Equation: Linking X and Y with Table Data

Continue Your Math Journey

Master Graphical Representation of a Function first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Ways to Represent a FunctionRepresenting a Function Verbally and with TablesAlgebraic Representation of a FunctionNotation of a FunctionRate of Change of a FunctionVariation of a FunctionRate of change represented with steps in the graph of the functionRate of change of a function represented graphicallyConstant Rate of ChangeVariable Rate of ChangeRate of Change of a Function Represented by a Table of ValuesFunctions for Seventh GradeIncreasing and Decreasing Intervals (Functions)Increasing functionsDecreasing functionConstant FunctionDecreasing Interval of a functionIncreasing Intervals of a functionDomain of a FunctionIndefinite integralInputing Values into a Function

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Creating a table from a verbal description Determine whether the table represents a function Is the graph an example of a function? Matching a graph to a function Matching a graph to a table Matching a table to a function Sketch the Graph from a Verbal Description