In which domain does the function increase? Green line: $$ x=-0.8 $$ –2 –2 –2 2 2 2 2 2 2 0 0 0

It does not have an increasing domain.

Increasing and Decreasing Intervals Practice Problems

Master function behavior with step-by-step practice problems on increasing, decreasing, and constant intervals. Learn to analyze quadratic and linear functions effectively.

📚Master Function Intervals with Interactive Practice

Find increasing and decreasing intervals for quadratic functions like f(x) = 5x² - 25
Identify vertex coordinates using the formula x = -b/(2a) for parabolas
Determine when functions are constant, increasing, or decreasing on given intervals
Analyze domain of positivity and negativity from function graphs
Apply interval notation to describe function behavior accurately
Solve real-world problems involving function monotonicity and optimization

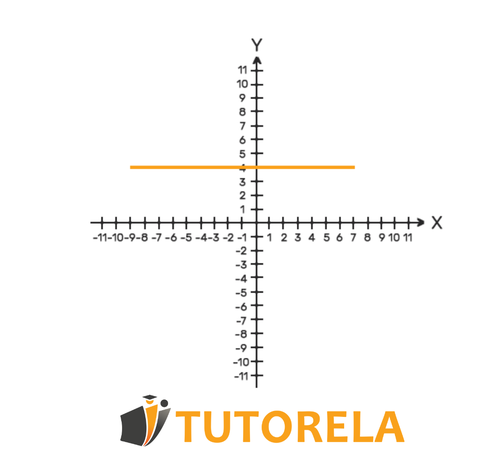
Understanding Constant Function

Complete explanation with examples

We will say that a function is constant when, as the value of the independent variable $X$ increases, the dependent variable $Y$ remains the same.

Let's assume we have two elements $X$ , which we will call $X1$ and $X2$ , where the following is true: $X1<X2$ , that is, $X2$ is located to the right of $X1$ .

When $X1$ is placed in the domain, the value $Y1$ is obtained.
When $X2$ is placed in the domain, the value $Y2$ is obtained.

The function is constant when: $X2>X1$ and also \(Y2=Y1).

The function can be constant in intervals or throughout its domain.

Constant Function

Detailed explanation

Practice Constant Function

Test your knowledge with 17 quizzes

In which interval does the function decrease?

Red line: $$ x=0.65 $$

Examples with solutions for Constant Function

Step-by-step solutions included

Exercise #1

In what domain does the function increase?

Step-by-Step Solution

Let's remember that the function increases if the $x$ values and $y$ values increase simultaneously.

On the other hand, the function decreases if the $x$ values increase while the $y$ values decrease simultaneously.

In the given graph, we can see that the function increases in the domain where $x > 0$ ; in other words, where the $y$ values are increasing.

Answer:

$x > 0$

Video Solution

Exercise #2

Determine in which domain the function is negative?

Step-by-Step Solution

Remember that a function is increasing if both X values and Y values are increasing simultaneously.

A function is decreasing if X values are increasing while Y values are decreasing simultaneously.

In the graph, we can observe that in the domain $x > 1$ the function is decreasing, meaning the Y values are decreasing.

Answer:

$x > 1$

Video Solution

Exercise #3

In what domain is the function increasing?

Step-by-Step Solution

Let's first remember that a function is increasing if both the X and Y values are increasing simultaneously.

Conversely, a function is decreasing if the X values are increasing while the Y values are decreasing simultaneously.

In the graph shown, we can see that the function is increasing in every domain and therefore the function is increasing for all values of X.

Answer:

All values of $x$

Video Solution

Exercise #4

In what domain does the function increase?

Step-by-Step Solution

Let's remember that the function increases if the X values and Y values increase simultaneously.

On the other hand, the function decreases if the X values increase and the Y values decrease simultaneously.

In the given graph, we notice that the function increases in the domain where $x < 0$ , meaning the Y values are increasing.

Answer:

$x<0$

Video Solution

Exercise #5

In what interval is the function increasing?

Purple line: $x=0.6$

Step-by-Step Solution

Let's remember that a function is described as increasing if both X values and Y values are increasing simultaneously.

A function is decreasing if X values are increasing while Y values are decreasing simultaneously.

In the graph, we can see that in the domain $x < 0.6$ the function is increasing, meaning the Y values are increasing.

Answer:

$x<0.6$

Video Solution

Frequently Asked Questions

Everything you need to know about Constant Function

How do you find increasing and decreasing intervals of a quadratic function?

For a quadratic function f(x) = ax² + bx + c, first find the vertex x-coordinate using x = -b/(2a). If a > 0, the function decreases for x < vertex and increases for x > vertex. If a < 0, the pattern reverses.

What makes a function constant on an interval?

A function is constant when the y-values remain the same as x increases. Mathematically, if x₁ < x₂ but f(x₁) = f(x₂), then the function is constant on that interval.

What is the difference between domain of positivity and increasing intervals?

Domain of positivity refers to x-values where f(x) > 0 (function is above x-axis). Increasing intervals refer to x-values where the function rises from left to right. These are completely different concepts.

How do you read increasing and decreasing intervals from a graph?

Look at the function from left to right: (1) Increasing where the graph goes upward, (2) Decreasing where the graph goes downward, (3) Constant where the graph is horizontal. Mark the x-values where direction changes.

Why is finding the vertex important for quadratic function intervals?

The vertex represents the turning point of a parabola. For upward-opening parabolas (a > 0), it's the minimum point where the function changes from decreasing to increasing. For downward-opening parabolas (a < 0), it's the maximum where function changes from increasing to decreasing.

Can a linear function have both increasing and decreasing intervals?

No, a non-horizontal linear function is either always increasing (positive slope) or always decreasing (negative slope) across its entire domain. Only horizontal lines (slope = 0) are constant.

What does interval notation look like for function behavior?

Use parentheses for open intervals: increasing on (0, ∞) means x > 0. Use brackets for closed intervals when endpoints are included. For example, decreasing on (-∞, 0] includes x = 0.

How do you handle piecewise functions when finding intervals?

Analyze each piece separately within its defined domain, then combine results. Check for continuity at boundary points and note any jumps or breaks that affect the overall interval classification.

Continue Your Math Journey

Master Constant Function first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Functions for Seventh Grade Increasing and Decreasing Intervals (Functions)Increasing functions Decreasing function Decreasing Interval of a function Increasing Intervals of a function Domain of a Function Indefinite integral Inputing Values into a Function

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Determine whether or not it is possible to create the function Determine whether the graph is increasing or decreasing Finding Increasing or Decreasing Domains Identifying increase and decrease from a verbal description of the function Identifying which domain is applicable for the described function Matching the graph to the story

Increasing and Decreasing Intervals Practice Problems

Understanding Constant Function

Practice Constant Function

Examples with solutions for Constant Function

Frequently Asked Questions

How do you find increasing and decreasing intervals of a quadratic function?

What makes a function constant on an interval?

What is the difference between domain of positivity and increasing intervals?

How do you read increasing and decreasing intervals from a graph?

Why is finding the vertex important for quadratic function intervals?

Can a linear function have both increasing and decreasing intervals?

What does interval notation look like for function behavior?

How do you handle piecewise functions when finding intervals?

More Constant Function Questions

Increasing and Decreasing Intervals of a Function

Continue Your Math Journey

Suggested Topics to Practice in Advance

Topics Learned in Later Sections

Practice by Question Type