In which domain does the function increase? Green line: $$ x=-0.8 $$ –2 –2 –2 2 2 2 2 2 2 0 0 0

It does not have an increasing domain.

Increasing and Decreasing Function Intervals Practice Problems

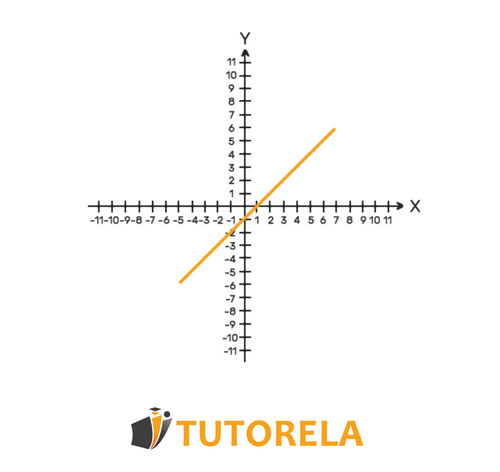
Understanding Increasing functions

Complete explanation with examples

Increasing functions

What is an Increasing Function?

An increasing function is a type of relationship where, as you move to the right on the graph (increasing the $x$ -value), the $y$ -value also gets bigger. It’s like climbing a hill—the higher you go (the more you increase $x$ ), the more your height (the $y$ -value) increases.

We will say that a function is increasing when, as the value of the independent variable $X$ increases, the value of the function $Y$ increases.

How to Spot an Increasing Function:

On a Graph: The line or curve goes upwards as you move from left to right.
In Numbers: For any two xxx-values, if the second number is larger than the first $x_2 > x_1$ , then the second $y$ -value will also be larger than the first $f(x_2) > f(x_1)$ .

Real-Life Example:

Think about saving money in a piggy bank. Every day you add more coins, and the total amount of money keeps going up. That’s an increasing function in action—your savings are the $y$ -values, and the number of days is the $x$ -values.

Fun Fact:

If the line or curve never stops going up, it's called strictly increasing. If it flattens for a bit before going up again, it's just increasing.

let's see an example of strictly increasing linear function:

Detailed explanation

Practice Increasing functions

Test your knowledge with 17 quizzes

In which interval does the function decrease?

Red line: $$ x=0.65 $$

Examples with solutions for Increasing functions

Step-by-step solutions included

Exercise #1

In what domain does the function increase?

Step-by-Step Solution

Let's remember that the function increases if the $x$ values and $y$ values increase simultaneously.

On the other hand, the function decreases if the $x$ values increase while the $y$ values decrease simultaneously.

In the given graph, we can see that the function increases in the domain where $x > 0$ ; in other words, where the $y$ values are increasing.

Answer:

$x > 0$

Video Solution

Exercise #2

Determine in which domain the function is negative?

Step-by-Step Solution

Remember that a function is increasing if both X values and Y values are increasing simultaneously.

A function is decreasing if X values are increasing while Y values are decreasing simultaneously.

In the graph, we can observe that in the domain $x > 1$ the function is decreasing, meaning the Y values are decreasing.

Answer:

$x > 1$

Video Solution

Exercise #3

In what domain is the function increasing?

Step-by-Step Solution

Let's first remember that a function is increasing if both the X and Y values are increasing simultaneously.

Conversely, a function is decreasing if the X values are increasing while the Y values are decreasing simultaneously.

In the graph shown, we can see that the function is increasing in every domain and therefore the function is increasing for all values of X.

Answer:

All values of $x$

Video Solution

Exercise #4

In what domain does the function increase?

Step-by-Step Solution

Let's remember that the function increases if the X values and Y values increase simultaneously.

On the other hand, the function decreases if the X values increase and the Y values decrease simultaneously.

In the given graph, we notice that the function increases in the domain where $x < 0$ , meaning the Y values are increasing.

Answer:

$x<0$

Video Solution

Exercise #5

In what interval is the function increasing?

Purple line: $x=0.6$

Step-by-Step Solution

Let's remember that a function is described as increasing if both X values and Y values are increasing simultaneously.

A function is decreasing if X values are increasing while Y values are decreasing simultaneously.

In the graph, we can see that in the domain $x < 0.6$ the function is increasing, meaning the Y values are increasing.

Answer:

$x<0.6$

Video Solution

Frequently Asked Questions

Everything you need to know about Increasing functions

What is the difference between increasing and decreasing functions?

+

An increasing function has y-values that get larger as x-values increase (moving left to right on a graph, the line goes up). A decreasing function has y-values that get smaller as x-values increase (the line goes down from left to right). Mathematically, a function is increasing when f(x₂) > f(x₁) whenever x₂ > x₁.

How do you find increasing intervals of a quadratic function?

+

For quadratic functions, find the vertex using x = -b/(2a). If a > 0 (parabola opens up), the function decreases before the vertex and increases after. If a < 0 (parabola opens down), the function increases before the vertex and decreases after. The vertex marks the transition point between increasing and decreasing intervals.

What does strictly increasing mean in mathematics?

+

A strictly increasing function continuously rises without any flat sections - it never stays constant or decreases. In contrast, a regular increasing function can have flat portions where it remains constant before continuing to increase. Strictly increasing functions have a steeper, more consistent upward trend.

How can you tell if a function is increasing from its graph?

+

Look at the direction of the line or curve as you move from left to right: • If it slopes upward, the function is increasing • If it slopes downward, the function is decreasing • If it's horizontal, the function is constant • Check specific intervals, as functions can increase in some areas and decrease in others

What are some real-world examples of increasing functions?

+

Common examples include: savings account balance over time (with regular deposits), height of a growing plant over months, temperature rising throughout a spring day, or distance traveled at constant speed over time. These all show one variable consistently increasing as another variable increases.

How do you solve y = -(x+3)² type problems for increasing intervals?

+

Step-by-step process: 1. Expand: y = -x² - 6x - 9 2. Identify coefficients: a = -1, b = -6, c = -9 3. Find vertex: x = -(-6)/(2×-1) = -3 4. Since a < 0, parabola opens down (maximum at vertex) 5. Function increases for x < -3 and decreases for x > -3

Why is the vertex important for finding increasing and decreasing intervals?

+

The vertex represents the turning point of a parabola - where the function changes from increasing to decreasing (or vice versa). For upward-opening parabolas (a > 0), the function decreases before the vertex and increases after. For downward-opening parabolas (a < 0), the function increases before the vertex and decreases after.

Can a function be both increasing and decreasing?

+

Yes, many functions have different intervals where they increase and decrease. For example, a parabola y = x² decreases for x < 0 and increases for x > 0. When analyzing functions, we identify specific intervals or domains where the function exhibits increasing or decreasing behavior, rather than describing the entire function with one term.

Continue Your Math Journey

Master Increasing functions first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Functions for Seventh Grade Increasing and Decreasing Intervals (Functions)Decreasing function Constant Function Decreasing Interval of a function Increasing Intervals of a function Domain of a Function Indefinite integral Inputing Values into a Function

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Determine whether or not it is possible to create the function Determine whether the graph is increasing or decreasing Finding Increasing or Decreasing Domains Identifying increase and decrease from a verbal description of the function Identifying which domain is applicable for the described function Matching the graph to the story

Increasing and Decreasing Function Intervals Practice Problems

Understanding Increasing functions

Increasing functions

What is an Increasing Function?

How to Spot an Increasing Function:

Real-Life Example:

Fun Fact:

Practice Increasing functions

Examples with solutions for Increasing functions

Frequently Asked Questions

What is the difference between increasing and decreasing functions?

How do you find increasing intervals of a quadratic function?

What does strictly increasing mean in mathematics?

How can you tell if a function is increasing from its graph?

What are some real-world examples of increasing functions?

How do you solve y = -(x+3)² type problems for increasing intervals?

Why is the vertex important for finding increasing and decreasing intervals?

Can a function be both increasing and decreasing?

More Increasing functions Questions

Increasing and Decreasing Intervals of a Function

Continue Your Math Journey

Suggested Topics to Practice in Advance

Topics Learned in Later Sections

Practice by Question Type