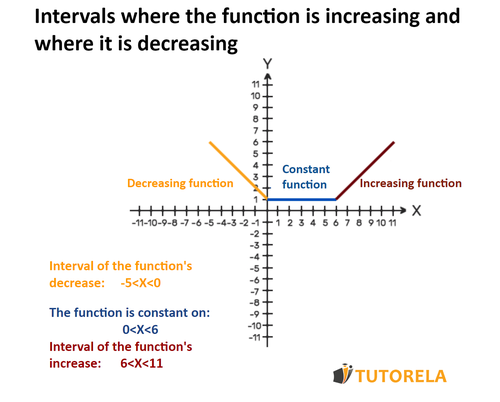
The intervals where the function is increasing show a certain situation in which the values of and increase together.
The intervals where the function is decreasing expose a certain situation in which the value of in a function increases while that of decreases.
In what domain does the function increase?
In what domain is the function negative?
In what domain is the function increasing?
In what domain does the function increase?
In what interval is the function increasing?
Purple line: \( x=0.6 \)
In what domain does the function increase?
Let's remember that the function increases if the X values and Y values increase simultaneously.
On the other hand, the function decreases if the X values increase and the Y values decrease simultaneously.
In the given graph, we notice that the function increases in the domain where x > 0 meaning the Y values are increasing.
x > 0
In what domain is the function negative?
Let's remember that a function is increasing if both X values and Y values are increasing simultaneously.
A function is decreasing if X values are increasing while Y values are decreasing simultaneously.
In the graph, we can see that in the domain x > 1 the function is decreasing, meaning the Y values are decreasing.
x > 1
In what domain is the function increasing?
Let's remember that a function is increasing if both X values and Y values are increasing simultaneously.
A function is decreasing if X values are increasing while Y values are decreasing simultaneously.
In the graph shown, we can see that the function is increasing in every domain, therefore the function is increasing for all X.
Entire
In what domain does the function increase?
Let's remember that the function increases if the X values and Y values increase simultaneously.
On the other hand, the function decreases if the X values increase and the Y values decrease simultaneously.
In the given graph, we notice that the function increases in the domain where x < 0 meaning the Y values are increasing.
x<0
In what interval is the function increasing?
Purple line:
Let's remember that a function is increasing if both X values and Y values are increasing simultaneously.
A function is decreasing if X values are increasing while Y values are decreasing simultaneously.
In the graph, we can see that in the domain x < 0.6 the function is increasing, meaning the Y values are increasing.
x<0.6
Determine the domain of the following function:
The function describes a student's grades throughout the year.
Which domain corresponds to the described function:
The function represents the velocity of a stone after being dropped from a great height as a function of time.
Determine the domain of the following function:
A function describing the charging of a computer battery during use.
Determine which domain corresponds to the function described below:
The function represents the height of a child from birth to first grade.
Determine which domain corresponds to the function described below:
The function represents the amount of fuel in a car's tank according to the distance traveled by the car.
Determine the domain of the following function:
The function describes a student's grades throughout the year.
According to logic, the student's grades throughout the year depend on many criteria that are not given to us.
Therefore, the appropriate domain for the function is - it is impossible to know.
Impossible to know.
Which domain corresponds to the described function:
The function represents the velocity of a stone after being dropped from a great height as a function of time.
According to logic, the speed of the stone during a fall from a great height will increase as it falls with acceleration.
In other words, the speed of the stone increases, so the appropriate domain for this function is - always increasing.
Always increasing
Determine the domain of the following function:
A function describing the charging of a computer battery during use.
According to logic, the computer's battery during use will always decrease since the battery serves as an energy source for the computer.
Therefore, the domain that suits this function is - always decreasing.
Always decreasing
Determine which domain corresponds to the function described below:
The function represents the height of a child from birth to first grade.
According to logic, a child's height from birth until first grade will always be increasing as the child grows.
Therefore, the domain that suits this function is - always increasing.
Always increasing.
Determine which domain corresponds to the function described below:
The function represents the amount of fuel in a car's tank according to the distance traveled by the car.
According to the definition, the amount of fuel in the car's tank will always decrease, since during the trip the car consumes fuel in order to travel.
Therefore, the domain that is suitable for this function is - always decreasing.
Always decreasing
Determine the domain of the following function:
The function represents the weight of a person over a period of 3 years.
In which interval does the function decrease?
Red line: \( x=0.65 \)
In what domain does the function increase?
Black line: \( x=1.1 \)
In which domain does the function decrease?
In what domain does the function increase?
Determine the domain of the following function:
The function represents the weight of a person over a period of 3 years.
Logically, a person's weight is something that fluctuates.
In one week, a person's weight can increase, but in the following week, it can decrease.
Therefore, the domain that suits this function is - partly increasing and partly decreasing.
Partly increasing and partly decreasing.
In which interval does the function decrease?
Red line:
Remember that a function is increasing if both X values and Y values are increasing simultaneously.
A function is decreasing if X values are increasing while Y values are decreasing simultaneously.
In the plotted graph, we can see that the function is decreasing in all domains. In other words, it is decreasing for all X.
All values of
In what domain does the function increase?
Black line:
Remember that a function is increasing if the X values and Y values are increasing simultaneously.
A function is decreasing if the X values are increasing and the Y values are decreasing simultaneously.
In the plotted graph, we can see that in the domain 1.1 > x > 0 the function is increasing, meaning the Y values are increasing.
1.1 > x > 0
In which domain does the function decrease?
Let's remember that a function is increasing if both X values and Y values are increasing simultaneously.
A function is decreasing if X values are increasing while Y values are decreasing simultaneously.
According to the value table, we can see that in the domain x < 2 , X values are increasing while Y values are decreasing simultaneously. Therefore, the function is decreasing in the domain x < 2
x<2
In what domain does the function increase?
Let's remember that the function increases if the X values and Y values increase simultaneously.
On the other hand, the function decreases if the X values increase and the Y values decrease simultaneously.
In the given graph, we notice that the function increases in the domain where 1 > x > -1 meaning the Y values are increasing.
1 > x > -1