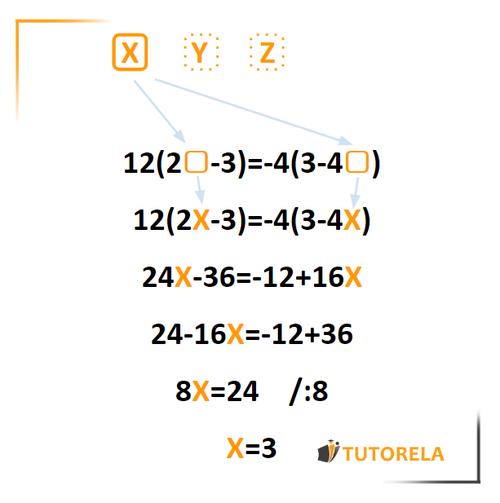
Equations are algebraic expressions containing numbers and unknowns. It is important to differentiate these two groups: the numbers are fixed values while the unknowns, as their name indicates, represent unknown values (at least at the beginning), and in most cases we are asked to find out what this value is.
For example: