Solving an equation using the distributive property is related to the need to open the parentheses as the first step to then be able to simplify similar members. When an equation contains one or more pairs of parentheses, we must start by opening them all and then proceed to the next phase.
Quadratic Equations Factoring Practice Problems
Master solving quadratic equations by factoring with step-by-step practice problems. Build confidence with guided examples and instant feedback.
- Factor quadratic expressions into two binomial terms
- Apply the zero product property to find equation solutions
- Solve quadratic equations of the form ax² + bx + c = 0
- Identify when factoring is the most efficient solution method
- Check solutions by substituting back into original equations
- Recognize patterns in quadratic expressions for faster factoring
Understanding Solving Quadratic Equations using Factoring
Below, we provide you with some examples where this method is applied.
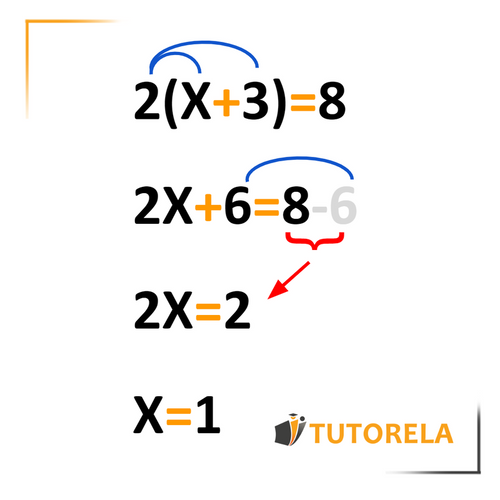
In this equation, we can clearly see some parentheses. To start, we must open them (that is, apply the distributive property) and then we can proceed with the following phases of the exercise.
The result of the equation is .
Practice Solving Quadratic Equations using Factoring
Solve for X:
\( \frac{1}{4}(x-8)=1 \)
Examples with solutions for Solving Quadratic Equations using Factoring
Solve for x:
To solve this equation, follow these steps:
Step 1: Apply the distributive property to the equation:
Step 2: Simplify the equation:
The equation now becomes:
Step 3: Isolate the variable by simplifying the equation:
First, subtract 8 from both sides:
This simplifies to:
Step 4: Solve for by dividing both sides by -2:
Therefore, the solution to the equation is .
Answer:
0
Solve for x:
To open parentheses we will use the formula:
We multiply accordingly
We will move the 35 to the right section and change the sign accordingly:
We solve the subtraction exercise on the right side and we will obtain:
We divide both sections by -14
Answer:
-3
Solve x:
We open the parentheses according to the formula:
We will move the 15 to the right section and keep the corresponding sign:
Divide both sections by 5
Answer:
To solve the linear equation , we'll proceed with the following steps:
Step 1: Apply the Distributive Property.
The equation given is .
First, distribute the 2 across the terms inside the parenthesis:
.
By substituting this back into the equation, we have:
.
Step 2: Combine Like Terms.
Now, combine the terms containing :
.
The equation now becomes:
.
Step 3: Isolate the Variable.
Add 14 to both sides of the equation to isolate terms with :
, which simplifies to:
.
Next, divide both sides by 14 to solve for :
.
Therefore, the solution to the equation is .
Answer:
Let's proceed to solve the linear equation :
Step 1: Distribute the 3 in the expression .
We get:
This simplifies to:
Step 2: Simplify the expression by combining like terms.
We simplify this to:
or simply
Step 3: Isolate by dividing both sides by 3.
Thus,
Therefore, the solution to the problem is .
The correct choice is the option corresponding to .
Answer: