Linear Equations One Variable Practice Problems & Solutions

Master solving linear equations with one variable through step-by-step practice problems. Learn isolation techniques, verification methods, and common solution strategies.

📚Master Linear Equations with One Variable Through Targeted Practice

Solve equations using addition and subtraction to isolate variables
Apply multiplication and division operations to clear coefficients and fractions
Verify solutions by substituting back into original equations
Handle equations with negative coefficients and zero on one side
Combine multiple operations to solve complex linear equations step-by-step
Identify and correct common mistakes in equation solving processes

Understanding Linear Equations (One Variable)

Complete explanation with examples

The solution for an equation is a numerical value that, when inserted in the place of the unknown (or the variable), will render both members of the equation equal, that is, we will obtain a "true statement". In first degree equations with one unknown, there can only be one solution.

Example:

$X - 1 = 5$

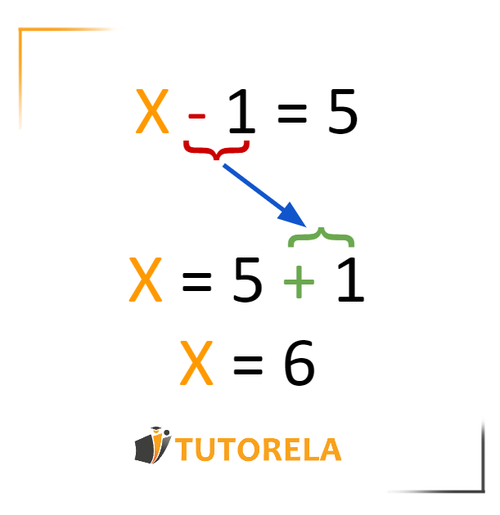
This is an equation with one unknown or variable indicated by the letter $X$ . The equation is composed of two members separated by the use of the equal sign $=$ . The left member is everything to the left of the sign $=$ , and the right member is everything to the right of the sign.

Our goal is to isolate the variable (or clear the variable) $X$ in order that it only remains in one of the members of the equation. In doing so we should be able to determine its value. In this article we will learn how to use the four mathematical operations(addition, subtraction, multiplication and division) to isolate the variable $X$ .

Detailed explanation

Practice Linear Equations (One Variable)

Test your knowledge with 42 quizzes

Solve for X:

$$ 3-x+7=5 $$

Examples with solutions for Linear Equations (One Variable)

Step-by-step solutions included

Exercise #1

Find the value of the parameter X

$-8-x=5$

Step-by-Step Solution

To solve the given linear equation $-8 - x = 5$ , we will follow these steps:

Add 8 to both sides of the equation to isolate the term involving $x$ .
Subtract $x$ from both sides to further simplify; however, applying approach 1 directly cancels this step.
Multiply both sides by -1 to solve for $x$ .

First, let's add 8 to both sides of the equation:

-8 - x + 8 = 5 + 8

This simplifies to:

-x = 13

To find $x$ , multiply both sides of the equation by -1:

x = -13

Therefore, the solution to the equation is $x = -13$ .

Answer:

$-13$

Video Solution

Exercise #2

Find the value of the parameter X:

$x+5=8$

Step-by-Step Solution

To solve the equation $x + 5 = 8$ , follow these steps:

Step 1: Start with the original equation:
$x + 5 = 8$ .
Step 2: Subtract 5 from both sides of the equation to isolate $x$ :
$x + 5 - 5 = 8 - 5$ .
Step 3: Simplify both sides:
$x = 3$ .

Therefore, the solution to the equation is $x = 3$ .

The correct answer choice is: :

Answer:

Video Solution

Exercise #3

Solve for $x$ :

$5x \cdot 3 = 45$

Step-by-Step Solution

To solve the equation $5x \cdot 3 = 45$ , follow these steps:

1. First, identify the operation needed to solve for $x$ . In this case, we have a multiplication equation.

2. Therefore, we divide both sides of the equation by 15 (since $5 \times 3 = 15$ ) to isolate $x$ :

$x = \frac{45}{15}$

3. Calculate $x$ :

$x = 3$

Answer:

$x=3$

Video Solution

Exercise #4

Solve for X:

$10+3x=19$

Step-by-Step Solution

To solve the equation $10 + 3x = 19$ , follow these steps:

Step 1: Subtract 10 from both sides of the equation to begin isolating $x$ :
$10 + 3x - 10 = 19 - 10$
This simplifies to $3x = 9$ .
Step 2: Divide both sides by 3 to solve for $x$ :
$\frac{3x}{3} = \frac{9}{3}$
This reduces to $x = 3$ .

Therefore, the solution to the problem is $x = 3$ .

Answer:

Video Solution

Exercise #5

Solve for X:

$24-8x=-2x$

Step-by-Step Solution

To solve the equation $24 - 8x = -2x$ , we need to isolate $x$ . Follow these steps:

Step 1: Move all terms involving $x$ to one side of the equation. Add $8x$ to both sides to get:
$24 = 8x - 2x$
Step 2: Simplify the equation by combining like terms on the right:
$24 = 6x$
Step 3: Solve for $x$ by dividing both sides by 6:
$x = \frac{24}{6}$
Step 4: Simplify the result:
$x = 4$

Therefore, the solution to the problem is $\mathbf{x = 4}$ .

Answer:

Video Solution

Frequently Asked Questions

Everything you need to know about Linear Equations (One Variable)

How do you solve a linear equation with one variable step by step?

To solve a linear equation with one variable: 1) Identify the variable to isolate, 2) Use inverse operations to move terms to opposite sides, 3) Simplify by combining like terms, 4) Verify your solution by substituting back into the original equation. Always perform the same operation on both sides to maintain equality.

What is the difference between solving X - 1 = 5 and 2X = 8?

For X - 1 = 5, you add 1 to both sides to get X = 6. For 2X = 8, you divide both sides by 2 to get X = 4. The first uses addition/subtraction to isolate the variable, while the second uses multiplication/division to eliminate the coefficient.

How do you check if your solution to a linear equation is correct?

Substitute your solution back into the original equation in place of the variable. If both sides of the equation are equal after performing the calculations, your solution is correct. For example, if X = 6 solves X - 1 = 5, then 6 - 1 = 5 gives us 5 = 5, which is true.

What operations can you use to isolate variables in linear equations?

You can use four basic operations to isolate variables: • Addition (to eliminate subtraction) • Subtraction (to eliminate addition) • Multiplication (to eliminate division/fractions) • Division (to eliminate multiplication/coefficients). Always apply the same operation to both sides of the equation.

How do you solve equations with fractions like (1/3)x = 5?

To solve equations with fractions, multiply both sides by the denominator to eliminate the fraction. For (1/3)x = 5, multiply both sides by 3: 3 × (1/3)x = 3 × 5, which simplifies to x = 15. Always verify by substituting back: (1/3) × 15 = 5 ✓

What does it mean when a linear equation has one solution?

A linear equation with one variable has exactly one solution because there's only one value that makes both sides equal. This is a fundamental property of first-degree equations. When you find this value and substitute it back, you get a true statement like 5 = 5.

How do you solve multi-step linear equations like 2x + 3 = 5?

For multi-step equations, work backwards using order of operations: 1) First, subtract 3 from both sides: 2x = 2, 2) Then divide both sides by 2: x = 1. Always handle addition/subtraction before multiplication/division when isolating the variable.

What are common mistakes when solving linear equations with one variable?

Common mistakes include: • Forgetting to apply operations to both sides • Making arithmetic errors during calculations • Not verifying the solution in the original equation • Confusing addition/subtraction with multiplication/division operations • Incorrectly handling negative signs and coefficients

More Linear Equations (One Variable) Questions

Click on any question to see the complete solution with step-by-step explanations

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Addition, subtraction, multiplication and division Worded problems Combining like terms Monomial Number of terms Domain of definition Using additional geometric shapes Decimal numbers Opening parentheses Using fractions Solving an equation by adding/subtracting from both sides Binomial Exercises with fractions One sided equations Rearranging Equations Solving an equation by multiplying/dividing both sides Equations with variables on both sides

Linear Equations One Variable Practice Problems & Solutions

Understanding Linear Equations (One Variable)

Practice Linear Equations (One Variable)

Examples with solutions for Linear Equations (One Variable)

Frequently Asked Questions

How do you solve a linear equation with one variable step by step?

What is the difference between solving X - 1 = 5 and 2X = 8?

How do you check if your solution to a linear equation is correct?

What operations can you use to isolate variables in linear equations?

How do you solve equations with fractions like (1/3)x = 5?

What does it mean when a linear equation has one solution?

How do you solve multi-step linear equations like 2x + 3 = 5?

What are common mistakes when solving linear equations with one variable?

More Linear Equations (One Variable) Questions

Solving Equations Using All Methods

Linear Equations (One Variable)

Solution of an Equation

Practice by Question Type

More Resources and Links