Parabola

The Parabola $y=ax^2+bx+c$

This function is a quadratic function and is called a parabola.

We will focus on two main types of parabolas: maximum and minimum parabolas.

Minimum Parabola

Also called smiling or happy.

A vertex is the minimum point of the function, where $Y$ is the lowest.

We can identify that it is a minimum parabola if the $a$ equation is positive.

1b - We can identify that it is a minimum parabola if the equation a is positive

Maximum Parabola

Also called sad or crying.

A vertex is the maximum point of the function, where $Y$ is the highest.

We can identify that it is a maximum parabola if the $a$ equation is negative.

To the parabola,

the vertex marks its highest point.

How do we find it?

Detailed explanation

Start practice

Test yourself on the quadratic function!

What is the value ofl coeficiente $$ a $$ in the equation?

$$ -x^2+7x-9 $$

Practice more now

Find the vertex of the parabola

One of the following two methods can be chosen:

The first method: using the formula for the vertex of the parabola

$X=\frac{-b}{2a}$

The value of $X$ that we receive will be replaced in the parabola function and we will obtain the value of $Y$ relevant.

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

What is the value of the coefficient $$ b $$ in the equation below?

$$ 3x^2+8x-5 $$

Question 2

What is the value of the coefficient $$ c $$ in the equation below?

$$ 4x^2+9x-2 $$

Question 3

$$ y=x^2 $$

The second method: using two symmetric points

The formula to find $X$ a vertex using two symmetric points is:

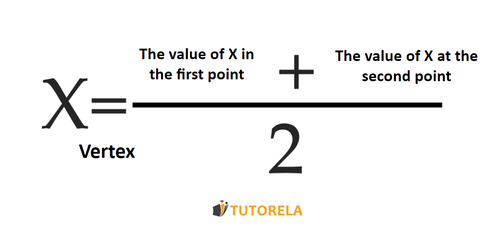
B3 - The formula to find X a vertex using two symmetric points

The vertex $X$ that we receive in the function to find the value of the vertex $Y$ .

Now, we will move on to the points of intersection of the parabola with the $X$ and $Y$ axes

Point of Intersection with the Axes

When we want to find the point of intersection with the $X$ axis:

We will set $Y=0$ in the quadratic equation and solve using a trinomial or the root formula.

We can find parabolas that are not zero and that do not have any point of intersection with the $X$ axis, or that have $1$ or a maximum of $2$ .

When we want to find a point of intersection with the $Y$ axis:

We will set $X=0$ in the quadratic equation and find the solutions.

Wonderful. Now we will move on to the areas of increase and decrease of the quadratic function.

Do you know what the answer is?

Question 1

$$ y=x^2+10x $$

Question 2

$$ y=x^2-6x+4 $$

Question 3

$$ y=2x^2-5x+6 $$

Areas of Increase and Decrease

The areas of increase and decrease describe the $X$ where the parabola increases and where the parabola decreases.

The parabola changes its domain once, at the vertex.

Let's see this in the figure:

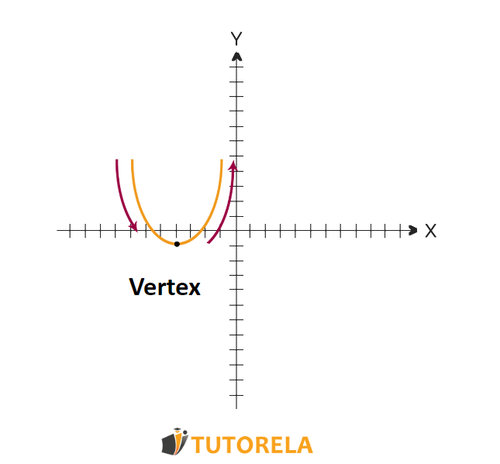
B4 - The areas of increase and decrease describe the X where the parabola increases decreases

When there is a graph:

We will examine what happens when the $X$ s are smaller than the vertex $X$ and what happens when the $X$ s are greater than the vertex $X$ .

When there is no graph:

We will examine the equation of the function and determine based on the coefficient of $X^2$ whether it is a minimum or maximum function.
Find the vertex $X$ according to the formula or by symmetric points.
We will plot a graph according to the data we have found and clearly see the areas of increase and decrease.

Positive and Negative Domains

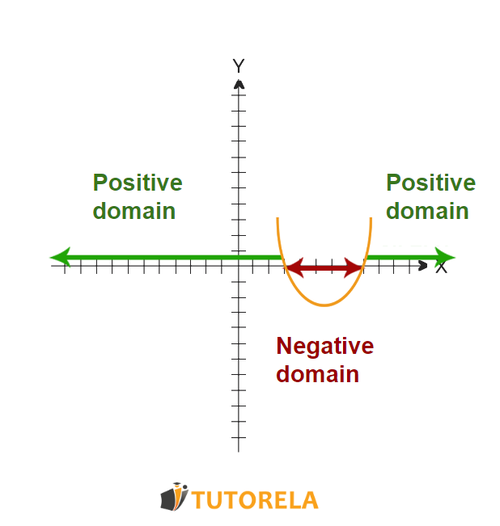
Positive domain: describes the $X$ where the graph of the parabola is above the $X$ axis, with a $Y$ value positive.

Negative domain: describes the $X$ where the graph of the parabola is below the $X$ axis, with a negative $Y$ value.

To find the domains of positivity and negativity, we will plot the graph of the parabola and ask:

At what $X$ values is the graph of the parabola above the $X$ axis, with a positive $Y$ value? This will be the domain of positivity of the parabola.

At what $X$ values is the graph of the parabola below the $X$ axis, with a negative $Y$ value? This will be the domain of negativity of the parabola.

Let's see this on the graph:

B5 - Positive domain and negative domain

We will find the points of intersection with the axes and mark them on the coordinate system.

Find the vertex of the parabola and mark it on the coordinate system.
We will understand if the parabola is a maximum or minimum (according to the coefficient $a$ ) and will draw accordingly.

Examples and exercises with solutions of parabola

Exercise #1

$y=x^2+10x$

Video Solution

Step-by-Step Solution

Here we have a quadratic equation.

A quadratic equation is always constructed like this:

$y = ax²+bx+c$

Where a, b, and c are generally already known to us, and the X and Y points need to be discovered.

Firstly, it seems that in this formula we do not have the C,

Therefore, we understand it is equal to 0.

$c = 0$

a is the coefficient of X², here it does not have a coefficient, therefore

$a = 1$

$b= 10$

is the number that comes before the X that is not squared.

Answer

$a=1,b=10,c=0$

Exercise #2

$y=2x^2-5x+6$

Video Solution

Step-by-Step Solution

In fact, a quadratic equation is composed as follows:

y = ax²-bx-c

That is,

a is the coefficient of x², in this case 2.
b is the coefficient of x, in this case 5.
And c is the number without a variable at the end, in this case 6.

Answer

$a=2,b=-5,c=6$

Exercise #3

What is the value of the coefficient $b$ in the equation below?

$3x^2+8x-5$

Video Solution

Step-by-Step Solution

The quadratic equation of the given problem is already arranged (that is, all the terms are found on one side and the 0 on the other side), thus we approach the given problem as follows;

In the problem, the question was asked: what is the value of the coefficient $b$ in the equation?

Let's remember the definitions of coefficients when solving a quadratic equation as well as the formula for the roots:

The rule says that the roots of an equation of the form

$ax^2+bx+c=0$ are :

$x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

That is the coefficient $b$ is the coefficient of the term in the first power - $x$ We then examine the equation of the given problem:

$3x^2+8x-5 =0$ That is, the number that multiplies

$x$ is

$8$ Consequently we are able to identify b, which is the coefficient of the term in the first power, as the number $8$ ,

Thus the correct answer is option d.

Answer

Exercise #4

What is the value of the coefficient $c$ in the equation below?

$3x^2+5x$

Video Solution

Step-by-Step Solution

The quadratic equation of the given problem has already been arranged (that is, all the terms are on one side and 0 is on the other side) thus we can approach the question as follows:

In the problem, the question was asked: what is the value of the coefficient $c$ in the equation?

Let's remember the definition of a coefficient when solving a quadratic equation as well as the formula for the roots:

The rule says that the roots of an equation of the form

$ax^2+bx+c=0$ are:

$x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

That is the coefficient
$c$ is the free term - and as such the coefficient of the term is raised to the power of zero - $x^0$ (Any number other than zero raised to the power of zero equals 1:

$x^0=1$ )

Next we examine the equation of the given problem:

$3x^2+5x=0$ Note that there is no free term in the equation, that is, the numerical value of the free term is 0, in fact the equation can be written as follows:

$3x^2+5x+0=0$ and therefore the value of the coefficient $c$ is 0.

Hence the correct answer is option c.

Answer

Exercise #5

$y=x^2$

Video Solution

Answer

$a=1,b=0,c=0$

Check your understanding

Question 1

$$ y=2x^2-3x-6 $$

Question 2

$$ y=-2x^2+3x+10 $$

Question 3

$$ y=3x^2+4x+5 $$

Start practice

The Parabola y=ax2+bx+c y=ax^2+bx+c y=ax2+bx+c

Minimum Parabola

Maximum Parabola

Test yourself on the quadratic function!

Find the vertex of the parabola

The first method: using the formula for the vertex of the parabola

The second method: using two symmetric points

Point of Intersection with the Axes

Areas of Increase and Decrease

Positive and Negative Domains

We will find the points of intersection with the axes and mark them on the coordinate system.

Examples and exercises with solutions of parabola

Exercise #1

Video Solution

Step-by-Step Solution

Answer

Exercise #2

Video Solution

Step-by-Step Solution

Answer

Exercise #3

Video Solution

Step-by-Step Solution

Answer

Exercise #4

Video Solution

Step-by-Step Solution

Answer

Exercise #5

Video Solution

Answer

The Parabola $y=ax^2+bx+c$