Perimeter: calculating the perimeter of a triangle
To calculate the perimeter of a triangle, all you have to do is add its three sides. If you have all the necessary information, you can solve such a problem in a matter of seconds, for example:
Formula for the perimeter of a triangle:
P = Side 1 + Side 2 + Side 3.
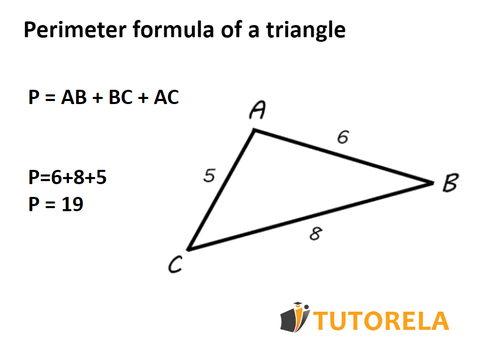
If you give us a triangle whose sides have the following measurements:
In this case, the perimeter of the triangle, which is the sum of the sides will be equal to.