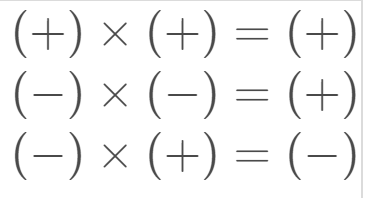Multiplication and Division of Signed Numbers Practice

Master positive and negative number operations with step-by-step practice problems. Learn sign rules for multiplying and dividing integers effectively.

📚Master Signed Number Operations with Interactive Practice

Apply sign rules to multiply positive and negative numbers correctly
Solve division problems with integers using same sign and different sign rules
Practice multi-step operations combining multiplication and division of signed numbers
Identify patterns in positive and negative number operations
Build confidence with real-world applications of signed number calculations
Master the fundamental laws of signs for all arithmetic operations

Understanding Multiplication and Division of Signed Mumbers

Complete explanation with examples

The method to solve an exercise with real numbers, when it involves multiplication and division, is very similar to the one we use when we have to add or subtract real numbers, with the difference that, in this case, we must make use of the multiplication and division table that we learned in elementary school.

When we have two real numbers with the same sign (plus or minus) we distinguish two cases:

The product (result of the multiplication) of two positive numbers will be positive. The quotient (result of the division) of two positive numbers will be positive.
$(+2) \times (+1)= +2$
$(+2) :(+1)= +2$
The product of two negative numbers will be positive. The quotient of two negative numbers will be positive.
$(-2) \times (-1)= +2$
$(-2) :(-1)= +2$
When we have two numbers with different signs, that is, one with the plus sign and the other with the minus sign, the result of the multiplication or division will always be negative.
$(+2) \times (-1)= -2$
$(-2) :(+1)= -2$

Detailed explanation

Practice Multiplication and Division of Signed Mumbers

Test your knowledge with 45 quizzes

Solve the following problem:

$$ -35:-7= $$

Examples with solutions for Multiplication and Division of Signed Mumbers

Step-by-step solutions included

Exercise #1

$(+4):(-1)=$

Step-by-Step Solution

Due to the fact that we are dividing a positive number by a negative number, the result must be a negative number:

$+:-=-$

Therefore:

$-(4:1)=-4$

Answer:

$-4$

Video Solution

Exercise #2

$(+9)\times(-4)=$

Step-by-Step Solution

Due to the fact that we are multiplying a positive number by a negative number, the result must be a negative number:

$+\times-=-$

Therefore:

$+9\times-4=-36$

Answer:

$-36$

Video Solution

Exercise #3

Solve the following exercise:

$(+6)\cdot(+9)=$

Step-by-Step Solution

Due to the fact that we are multiplying two positive numbers the result will also be positive:

$+\times+=+$

We obtain the following:

$+6\times+9=+54=54$

Answer:

$54$

Exercise #4

Solve the following exercise:

$(+5)\cdot(+5)=$

Step-by-Step Solution

Due to the fact that we are multiplying two positive numbers together, the result will inevitably be positive:

$+\times+=+$

We obtain the following result:

$+5\times+5=+25=25$

Answer:

$25$

Exercise #5

Solve the following exercise:

$(+9)\cdot(+4)=$

Step-by-Step Solution

Note that we are multiplying two positive numbers, so the result will necessarily be positive:

$+\times+=+$

We get:

$+9\times+4=+36=36$

Answer:

$36$

Frequently Asked Questions

Everything you need to know about Multiplication and Division of Signed Mumbers

What are the basic sign rules for multiplying positive and negative numbers?

When multiplying signed numbers: same signs give positive results (+ × + = +, - × - = +), while different signs give negative results (+ × - = -, - × + = -). This fundamental rule applies to all integer multiplication problems.

How do you divide negative numbers step by step?

Follow these steps: 1) Identify the signs of both numbers, 2) Apply the sign rule (same signs = positive, different signs = negative), 3) Divide the absolute values normally, 4) Apply the determined sign to your answer.

Why does multiplying two negative numbers give a positive result?

This follows the mathematical principle that multiplication by a negative number reverses direction on the number line. When you reverse direction twice (multiply by two negatives), you end up moving in the original positive direction.

What's the difference between multiplying and dividing signed numbers?

Both operations follow identical sign rules: same signs produce positive results, different signs produce negative results. The only difference is the arithmetic operation itself (multiplication tables vs. division facts).

How do you solve problems with multiple signed number operations?

Work from left to right, applying sign rules at each step: (+10) × (-5) × (-3) = (-50) × (-3) = (+150). Group operations when possible and always determine the sign before calculating the numerical value.

What are common mistakes students make with signed number operations?

Common errors include: confusing addition/subtraction rules with multiplication/division rules, forgetting that two negatives make a positive, and not properly tracking signs in multi-step problems. Practice with systematic sign checking prevents these mistakes.

Can you use fractions and decimals with signed number multiplication and division?

Yes, the same sign rules apply to all real numbers including fractions and decimals. For example: (-2.5) × (+4) = -10, and (-1/2) ÷ (-1/4) = +2. The sign rules remain consistent regardless of number type.

How do signed number operations apply to real-world problems?

Signed numbers appear in temperature changes, financial calculations (profit/loss), elevation changes, and physics problems involving direction. Understanding these operations helps solve practical problems involving opposite quantities or directional changes.

More Multiplication and Division of Signed Mumbers Questions

Click on any question to see the complete solution with step-by-step explanations

Multiplication and Division of Signed Mumbers

Continue Your Math Journey

Master Multiplication and Division of Signed Mumbers first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Integers

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Complete the equation Complete the following equation using the appropriate signs Complete the missing number Complete the missing numbers Determine the reciprocal of the given number Determine the resulting sign from the exercise Dividing a negative number by 1 and (-1) Dividing numbers with different signs Division between negative numbers Division by 0 Division of positive numbers Multiplication of a negative number by a neutral number Multiplication of a negative number by a positive number Multiplication of negative numbers Multiplication of positive numbers Multiplication of signed numbers Solving the problem Substituting parameters Using order of arithmetic operations Worded problems

Multiplication and Division of Signed Numbers Practice

Understanding Multiplication and Division of Signed Mumbers

Practice Multiplication and Division of Signed Mumbers

Examples with solutions for Multiplication and Division of Signed Mumbers

Frequently Asked Questions

What are the basic sign rules for multiplying positive and negative numbers?

How do you divide negative numbers step by step?

Why does multiplying two negative numbers give a positive result?

What's the difference between multiplying and dividing signed numbers?

How do you solve problems with multiple signed number operations?

What are common mistakes students make with signed number operations?

Can you use fractions and decimals with signed number multiplication and division?

How do signed number operations apply to real-world problems?

More Multiplication and Division of Signed Mumbers Questions

Multiplication and Division of Signed Mumbers

Continue Your Math Journey

Suggested Topics to Practice in Advance

Topics Learned in Later Sections

Practice by Question Type