What will be the sign of the result of the next exercise?
Multiplication and Division of Signed Mumbers: Determine the resulting sign from the exercise
What will be the sign of the result of the next exercise?
\( (-2)\cdot(-4)= \)
What will be the sign of the result of the next exercise?
\( (-2)\cdot(-\frac{1}{2})= \)
What will be the sign of the result of the next exercise?
\( (-4)\cdot12= \)
Will the result of the exercise below be positive or negative?
\( 5\cdot(-\frac{1}{2})= \)
What will be the sign of the result of the next exercise?
\( (-3)\cdot(-4)= \)
Examples with solutions for Multiplication and Division of Signed Mumbers: Determine the resulting sign from the exercise
Exercise #1
Video Solution
Step-by-Step Solution
It's important to remember: when we multiply a negative by a negative, the result is positive!
You can use this guide:
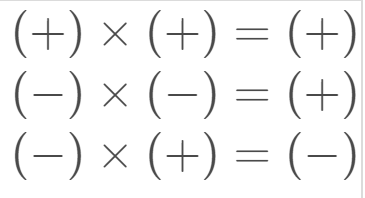
Answer
Positive
Exercise #2
What will be the sign of the result of the next exercise?
Video Solution
Step-by-Step Solution
Let's recall the law:
Therefore, the sign of the exercise result will be positive:
Answer
Positive
Exercise #3
What will be the sign of the result of the next exercise?
Video Solution
Step-by-Step Solution
Let's remember the rule:
Therefore, the sign of the exercise result will be negative:
Answer
Negative
Exercise #4
Will the result of the exercise below be positive or negative?
Video Solution
Step-by-Step Solution
Let's remember the rule:
Therefore, the sign of the exercise result will be negative:
Answer
Negative
Exercise #5
What will be the sign of the result of the next exercise?
Video Solution
Step-by-Step Solution
Let's remember the rule:
Therefore, the sign of the exercise result will be positive:
Answer
Positive
What will be the sign of the result of the next exercise?
\( 6\cdot3= \)
What will be the sign of the result of the next exercise?
\( (-6)\cdot5= \)
What will be the sign of the result of the next exercise?
\( (-16)\cdot(-5)= \)
What will be the sign of the result of the next exercise?
\( 2\cdot(-2)= \)
Determine the resulting sign of the following exercise:
\( \frac{1}{4}\cdot\frac{1}{2}= \)
Exercise #6
What will be the sign of the result of the next exercise?
Video Solution
Step-by-Step Solution
Let's remember the rule:
Therefore, the sign of the exercise result will be positive:
Answer
Positive
Exercise #7
What will be the sign of the result of the next exercise?
Video Solution
Step-by-Step Solution
Remember the law:
For the sum of the angles of a triangle is always:
Answer
Negative
Exercise #8
What will be the sign of the result of the next exercise?
Video Solution
Step-by-Step Solution
To determine the sign of the expression , we follow these logical steps:
- Step 1: Identify the signs of the numbers involved. Both numbers and are negative.
- Step 2: Apply the rule for multiplication of signed numbers: The product of two numbers with the same sign (both negative) is always positive.
Therefore, the sign of the result for the expression is Positive.
Answer
Positive
Exercise #9
What will be the sign of the result of the next exercise?
Video Solution
Step-by-Step Solution
To solve the exercise you need to remember an important rule: Multiplying a positive number by a negative number results in a negative number.
Therefore, if we multiply negative 2 by 2 the result will be negative 4.
That is, the result is negative.
Answer
Negative
Exercise #10
Determine the resulting sign of the following exercise:
Video Solution
Step-by-Step Solution
When there is no minus or plus sign before the numbers, we usually assume that these are positive numbers as shown below:
(+1/4)*(+1/2)=
The dot in the middle represents multiplication:
So the question in other words is - what happens when we multiply two positive numbers together?
We know that two positive integers when multiplied result in a positive integer:
Therefore the answer is "positive".
Answer
Positive
Determine the resulting sign from the following exercise:
\( (+3\frac{1}{4}):(+\frac{2}{5}) \)
Determine the resulting sign from the following exercise?
\( (+7.5):(+3) \)
What will be the sign of the result?
\( \frac{-4}{-0.4}:-1.7 \)
Will the result of the exercise below be positive (+) or negative (-)?
\( \frac{-4}{-8}:0.7 \)
What will be the sign of the result of the exercise?
\( \frac{-0.9}{1.1}:(-4) \)
Exercise #11
Determine the resulting sign from the following exercise:
Video Solution
Step-by-Step Solution
We will only look at whether the number is negative or positive.
In other words, the division exercise looks like this:
Since we are dividing a positive number by a positive number, our result must be positive.
Answer
+
Exercise #12
Determine the resulting sign from the following exercise?
Video Solution
Step-by-Step Solution
We will only look at whether the number is negative or positive.
In other words, the division exercise looks like this:
Since we are dividing a positive number by a positive number, the result must be a positive number.
Answer
+
Exercise #13
What will be the sign of the result?
Video Solution
Step-by-Step Solution
In this question, we only need to know whether the resulting number is negative or positive.
In that case, we can rewrite the division exercise as follows:
If we solve the exercise from left to right, we will first divide the numerator of the negative fraction by the denominator of the negative fraction.
Therefore, the resulting fraction will be positive:
Now the remaining exercise will look like this:
Therefore, the sign of the result will be negative.
Answer
-
Exercise #14
Will the result of the exercise below be positive (+) or negative (-)?
Video Solution
Step-by-Step Solution
In this question, we only need to work out whether the resulting value is negative or positive.
In other words, the division exercise can be considered as follows:
If we solve the exercise from left to right, we first divide the numerator of the negative fraction by the denominator of the negative fraction:
This leaves us with:
Therefore, the result of the exercise will be positive.
Answer
+
Exercise #15
What will be the sign of the result of the exercise?
Video Solution
Step-by-Step Solution
Let's see if the number is negative or positive.
As you can see, in the expression the numerator is negative and the denominator is positive.
That is, the division exercise will look like this:
The result of the expression will be a negative number, since we are dividing a negative number by a positive number.
Therefore, the exercise that will be obtained will look like this:
Therefore, the sign of the result of the exercise will be negative.
Answer
+
Determine the resulting sign of the following exercise:
\( 0:(-\frac{1}{8}) \)
Will the exercise result in a negative or a positive sign:
\( -\frac{4}{-0.4}:-1.7 \)
What will be the sign of the result of the exercise?
\( -\frac{9}{4}\cdot\frac{1}{2}\cdot\frac{10}{3} \)
What will be the sign of the result of the exercise?
\( 24:-8:12.4 \)
What will be the resulting sign from the following exercise?
\( (-7):(-\frac{3}{5}) \)
Exercise #16
Determine the resulting sign of the following exercise:
Video Solution
Step-by-Step Solution
Note the rule that anything we divide by zero will give us a result of zero:
Therefore, the answer is zero.
Answer
0
Exercise #17
Will the exercise result in a negative or a positive sign:
Video Solution
Step-by-Step Solution
We are only concentrating on whether the number is negative or positive.
In other words, the exercise should look like this:
If we solve the exercise from left to right, we must first multiply the fraction:
Since the numerator of the fraction is positive and divides by the negative denominator, the resulting fraction will be negative.
Therefore the remaining exercise is as follows:
If we then multiply minus by minus, we should obtain a positive number:
The resulting exercise is:
Therefore, the resulting sign of the exercise will be negative.
Answer
-
Exercise #18
What will be the sign of the result of the exercise?
Video Solution
Step-by-Step Solution
We will look only at whether the fraction is negative or positive.
In other words, the multiplication exercise looks like this:
If we solve the exercise from left to right, we'll first multiply minus by plus:
Now the remaining exercise is:
Therefore, the sign of the exercise result will be negative.
Answer
-
Exercise #19
What will be the sign of the result of the exercise?
Video Solution
Step-by-Step Solution
We will only look at whether the number is negative or positive.
In other words, the division exercise looks like this:
If we solve the exercise from left to right, we will first divide plus by minus:
Now the remaining exercise is:
Therefore, the sign of the exercise result will be negative.
Answer
-
Exercise #20
What will be the resulting sign from the following exercise?
Video Solution
Step-by-Step Solution
We will only look at whether the number is negative or positive.
In other words, the division exercise looks like this:
Since we are dividing a negative number by a negative number, the result must be a positive number.
Answer
+