Addition and Subtraction of Directed Numbers Practice

Understanding Addition and Subtraction of Directed Numbers

Complete explanation with examples

The addition and subtraction of real numbers are based on certain key principles. All principles will be explained using two real numbers, but certainly, the numbers in the exercise do not influence the method of resolution, therefore, these principles can be applied to any number in the exercise.

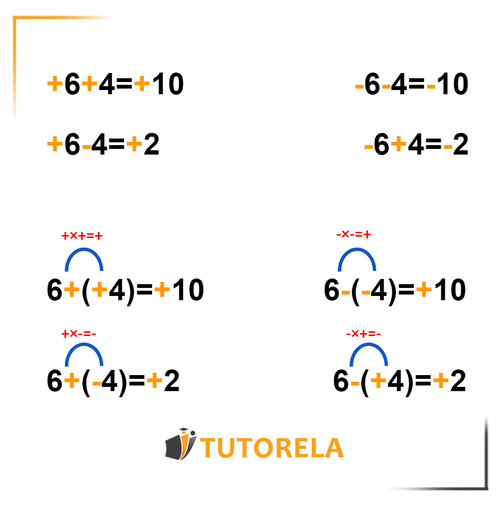
A1 - Addition and Subtraction of Real Numbers

When we have two real numbers with the same sign (plus or minus), this sign will remain in the result, which will, in fact, be the result of the addition. That is, if both numbers have a plus sign the result of the addition will also be positive. If both numbers have a minus sign the result of the subtraction will also be negative.
$+6+4=+10$
$-6-4=-10$

When we have two numbers with different signs it is crucial to determine which of the two has the greater absolute value (absolute: the distance from zero). The larger number will determine the sign of the result and, in fact, we will perform a subtraction operation.
$+6-4=+2$
$-6+4=-2$

When we have an exercise with a sequence of two signs (usually separated by parentheses) we will differentiate between several cases:

When the sequence is of two plus signs the result will also be positive
$6+(+4)=+10$

When the sequence is of two minus signs the result will also be positive
$6-(-4)=+10$

When the sequence is of minus and plus or of plus and minus the result will be negative.
$6+(-4)=+2$
$6-(+4)=+2$

Detailed explanation

Practice Addition and Subtraction of Directed Numbers

Test your knowledge with 31 quizzes

$$ 5+(-2)= $$

Examples with solutions for Addition and Subtraction of Directed Numbers

Step-by-step solutions included

Exercise #1

Solve the following expression using the number line below:

$14+(-19)=$

Step-by-Step Solution

Let's begin by locating the number 14 on the number line.

Let's proceed to handle the operation in the exercise, given that the operation is $+(-19)$

Since minus 19 is less than 0, we will move nineteen steps to the left from the number 14, where each step represents one whole number as follows:

We can see that the number we reached is minus 5.

Answer:

$-5$

Video Solution

Exercise #2

Solve the following expression using the number line below:

$(-10)+3=$

Step-by-Step Solution

Let's first locate negative 10 on the number line.

Now let's handle the operation in the exercise, given that the operation is $+3$

Since the number 3 is greater than 0, we will move three steps to the right from negative 10, where each step represents one whole number as follows:

We can see that the number we reached is negative 7.

Answer:

$-7$

Video Solution

Exercise #3

Solve the following expression using the number line below:

$(-13)+(-12)=$

Step-by-Step Solution

Let's first locate negative 13 on the number line.

Now let's deal with the operation in the exercise, given that the operation is $+(-12)$

Since negative 12 is less than 0, we will move twelve steps to the left from negative 13, where each step represents one whole number as follows:

We can see that the number we reached is negative 25.

Answer:

$-25$

Video Solution

Exercise #4

Solve the following expression using the number line below:

$5+(-13)=$

Step-by-Step Solution

Let's first locate the number 5 on the number line.

Now let's deal with the operation in the exercise, given that the operation is $+(-13)$

Since the number minus 13 is less than 0, we will move thirteen steps to the left from the number 5, where each step represents one whole number as follows:

We can see that the number we reached is minus 8.

Answer:

$-8$

Video Solution

Exercise #5

Solve the following equation using the number line below:

$(-14)+(-13)=$

Step-by-Step Solution

Let's first locate the number negative 14 on the number line.

Now let's look at the operation in the exercise, since the operation is $+(-13)$

Given that negative 13 is less than 0, we will move thirteen steps to the left from negative 14, where each step represents one whole number as follows:

We can see that the number we reached is negative 27.

Answer:

$-27$

Video Solution

Frequently Asked Questions

Everything you need to know about Addition and Subtraction of Directed Numbers

What happens when you add two negative numbers together?

+

When adding two negative numbers, the result is always negative. You add their absolute values and keep the negative sign. For example: (-6) + (-4) = -10.

How do you subtract a negative number from a positive number?

+

When subtracting a negative number, it becomes addition. The two negative signs create a positive sign. For example: 12 - (-2) = 12 + 2 = 14.

What is the elevator method for directed numbers?

+

The elevator method visualizes number operations as moving up and down floors. Positive numbers move up, negative numbers move down. Start at your first number's floor and follow each operation to reach the final answer.

How do you handle consecutive signs in directed number problems?

+

For consecutive signs: (++) = +, (--) = +, (+-) = -, (-+) = -. Two same signs become positive, two different signs become negative. Then solve the simplified expression normally.

When adding numbers with different signs, which sign wins?

+

The number with the larger absolute value determines the sign of the result. Subtract the smaller absolute value from the larger one, and use the sign of the number with larger absolute value.

What are the basic rules for directed number operations?

+

Key rules include: 1) Same signs: add absolute values, keep the sign, 2) Different signs: subtract absolute values, use sign of larger number, 3) Double negatives become positive, 4) Group operations to simplify expressions.

How do you simplify expressions with multiple directed numbers?

+

First, resolve any consecutive signs using sign rules. Then group similar operations together. Finally, work from left to right, applying addition and subtraction rules for positive and negative numbers.

What's the difference between absolute value and directed numbers?

+

Absolute value is the distance from zero (always positive), while directed numbers include both positive and negative values with their signs. In operations, you often compare absolute values to determine the result's sign.

More Addition and Subtraction of Directed Numbers Questions

Click on any question to see the complete solution with step-by-step explanations