Triangle Area Calculation: Finding Area with Base 5 and Height 6
Triangle Area with Base-Height Method
What is the area of the given triangle?
❤️ Continue Your Math Journey!
We have hundreds of course questions with personalized recommendations + Account 100% premium
Step-by-step video solution
Step-by-step written solution
Understand the problem
What is the area of the given triangle?
Step-by-step solution
This question is a bit confusing. We need start by identifying which parts of the data are relevant to us.
Remember the formula for the area of a triangle:
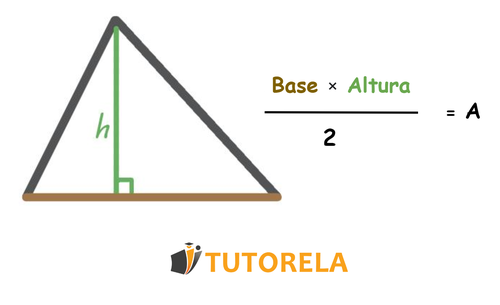The height is a straight line that comes out of an angle and forms a right angle with the opposite side.
In the drawing we have a height of 6.
It goes down to the opposite side whose length is 5.
And therefore, these are the data points that we will use.
We replace in the formula:
Final Answer
15
Key Points to Remember
- Formula: Area = (base × height) ÷ 2 for any triangle
- Technique: Use perpendicular height: (5 × 6) ÷ 2 = 15
- Check: Height must be perpendicular to base you choose ✓
Common Mistakes
- Using the wrong side as height Don't use side length 9 as height = Area of 22.5 instead of 15! The height must be perpendicular (90°) to the base, not just any side length. Always identify the perpendicular line from vertex to opposite side.
Practice Quiz
Calculate the area of the right triangle below:
FAQ
Why can't I use the side length of 9 as the height?
+The height must be perpendicular to the base! Side length 9 is slanted, not at a 90° angle to the base. Only the vertical line marked as 6 forms a right angle with the base.
How do I know which line is the height?
+Look for the dashed or dotted line that forms a right angle (90°) with one side. In this triangle, the vertical line of length 6 is perpendicular to the horizontal base of length 5.
Does it matter which side I choose as the base?
+No! You can choose any side as the base, but you must use the perpendicular height to that base. Different base-height pairs will give the same area.
What if the triangle looks different but has the same measurements?
+The area formula works for all triangles! Whether it's right, acute, or obtuse, as long as you have a base and its perpendicular height, use Area = (base × height) ÷ 2.
Why do we divide by 2 in the triangle area formula?
+A triangle is half of a rectangle! If you imagine completing the rectangle using the same base and height, the triangle takes up exactly half that space.
🌟 Unlock Your Math Potential
Get unlimited access to all 18 Triangle questions, detailed video solutions, and personalized progress tracking.
Unlimited Video Solutions
Step-by-step explanations for every problem
Progress Analytics
Track your mastery across all topics
Ad-Free Learning
Focus on math without distractions
No credit card required • Cancel anytime