Rectangle Properties Practice Problems for 9th Grade Students

Master rectangle properties, diagonals, and area calculations with step-by-step practice problems. Perfect for 9th grade geometry students learning quadrilaterals.

📚Master Rectangle Properties Through Interactive Practice
  • Identify and apply the five key properties of rectangles in geometry problems
  • Calculate rectangle areas using length and width measurements
  • Prove that quadrilaterals are rectangles using angle and diagonal tests
  • Solve problems involving rectangle diagonals and their intersection points
  • Apply rectangle properties to find missing side lengths and dimensions
  • Distinguish rectangles from other parallelograms using specific characteristics

Understanding Rectangles for Ninth Grade

Complete explanation with examples

Properties of a Rectangle

A rectangle is a quadrilateral with two pairs of parallel opposite edges (sides), the angles of which all equal 90 degrees.

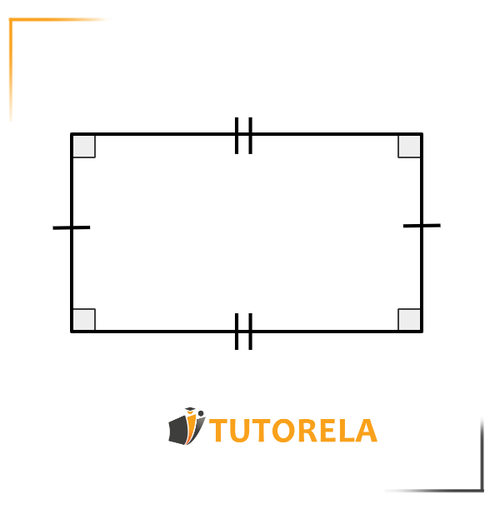
B- Properties of a Rectangle
  1. The pairs of sides in a rectangle are opposite, equal, and parallel.
  2. Each of the angles in a rectangle are equal to 90 degrees.
  3. The diagonals of a rectangle are equal.
  4. The diagonals of a rectangle intersect and do so at the midpoint of each other.
  5. Since the diagonals are equal, so are their halves.

Note:
The diagonals of a rectangle are not perpendicular (they are oblique) and do not cross the angles of the rectangle.

Detailed explanation

Practice Rectangles for Ninth Grade

Test your knowledge with 38 quizzes

The width of a rectangle is equal to 15 cm and its length is 3 cm.

Calculate the area of the rectangle.

Examples with solutions for Rectangles for Ninth Grade

Step-by-step solutions included
Exercise #1

Look at the rectangle ABCD below.

Side AB is 6 cm long and side BC is 4 cm long.

What is the area of the rectangle?
666444AAABBBCCCDDD

Step-by-Step Solution

Remember that the formula for the area of a rectangle is width times height

 

We are given that the width of the rectangle is 6

and that the length of the rectangle is 4

 Therefore we calculate:

6*4=24

Answer:

24 cm²

Video Solution
Exercise #2

Look at the rectangle ABCD below.

Side AB is 4.5 cm long and side BC is 2 cm long.

What is the area of the rectangle?
4.54.54.5222AAABBBCCCDDD

Step-by-Step Solution

We begin by multiplying side AB by side BC

We then substitute the given data and we obtain the following:

4.5×2=9 4.5\times2=9

Hence the area of rectangle ABCD equals 9

Answer:

9 cm²

Video Solution
Exercise #3

Look at rectangle ABCD below.

Side AB is 10 cm long and side BC is 2.5 cm long.

What is the area of the rectangle?
1010102.52.52.5AAABBBCCCDDD

Step-by-Step Solution

Let's begin by multiplying side AB by side BC

If we insert the known data into the above equation we should obtain the following:

10×2.5=25 10\times2.5=25

Thus the area of rectangle ABCD equals 25.

Answer:

25 cm²

Video Solution
Exercise #4

Look at the rectangle below.

Side AB is 2 cm long and side BC has a length of 7 cm.

What is the perimeter of the rectangle?
222777AAABBBCCCDDD

Step-by-Step Solution

Given that in a rectangle every pair of opposite sides are equal to each other, we can state that:

AB=CD=2 AB=CD=2

AD=BC=7 AD=BC=7

Now we can add all the sides together and find the perimeter:

2+7+2+7=4+14=18 2+7+2+7=4+14=18

Answer:

18 cm

Video Solution
Exercise #5

Look at the rectangle below.

Side DC has a length of 1.5 cm and side AD has a length of 9.5 cm.

What is the perimeter of the rectangle?

1.51.51.5AAABBBCCCDDD9.5

Step-by-Step Solution

Since in a rectangle every pair of opposite sides are equal to each other, we can state that:

AD=BC=9.5 AD=BC=9.5

AB=CD=1.5 AB=CD=1.5

Now we can add all the sides together and find the perimeter:

1.5+9.5+1.5+9.5=19+3=22 1.5+9.5+1.5+9.5=19+3=22

Answer:

22 cm

Video Solution

Frequently Asked Questions

Everything you need to know about Rectangles for Ninth Grade

What are the 5 main properties of a rectangle?

+
The five main properties are: (1) opposite sides are parallel and equal, (2) all angles measure 90 degrees, (3) diagonals are equal in length, (4) diagonals bisect each other at their midpoint, and (5) opposite sides are congruent. These properties distinguish rectangles from other quadrilaterals.

How do you prove a quadrilateral is a rectangle?

+
There are two main methods: First, check if three angles measure 90° (the fourth will automatically be 90°). Second, prove it's a parallelogram first, then show either one angle is 90° or the diagonals are equal in length.

Are the diagonals of a rectangle perpendicular?

+
No, the diagonals of a rectangle are NOT perpendicular. They are equal in length and bisect each other, but they intersect at oblique angles, not right angles. This is a common misconception among students.

What is the difference between a rectangle and a parallelogram?

+
A rectangle is a special type of parallelogram where all angles are 90 degrees. While parallelograms have opposite sides parallel and equal, rectangles have the additional requirement of right angles and equal diagonals.

How do you find the area of a rectangle?

+
The area of a rectangle equals length × width (or base × height). For example, if a rectangle has a length of 8 cm and width of 5 cm, the area is 8 × 5 = 40 cm². This formula works because rectangles have right angles.

Can a rectangle have unequal diagonals?

+
No, rectangles always have equal diagonals. If a quadrilateral has unequal diagonals, it cannot be a rectangle. Equal diagonals are one of the defining properties that distinguish rectangles from other parallelograms.

What happens when rectangle diagonals intersect?

+
When rectangle diagonals intersect, they bisect each other at their midpoint, creating four equal segments. If the diagonals are AC and BD intersecting at point E, then AE = BE = CE = DE. However, the diagonals don't form right angles.

How do you solve rectangle word problems step by step?

+
Follow these steps: (1) Identify given information (dimensions, area, perimeter), (2) write the appropriate formula (area = length × width), (3) substitute known values, (4) solve for the unknown variable, and (5) check your answer makes sense in context.

More Rectangles for Ninth Grade Questions

Click on any question to see the complete solution with step-by-step explanations

Rectangles

Calculate Rectangle Perimeter: Finding the Total Length of a 4.8 cm × 12 cm Rectangle Calculate the Perimeter: Finding Border Length in a 2×4×5 Rectangular Diagram Rectangle Area Problem: Finding BC When AB = 5cm and Area = 30cm² Calculate Rectangle Side Length: Given Area 42 cm² and Height 12 cm Find X in Rectangle: Area 40 cm² with Side Length 2x+4

Area of a Rectangle

Rectangle Area: Solving with Width x and Length x/2 When x=4 Calculate Rectangle Area: 3² cm Width × 1.5 cm Length Calculate Rectangle Area with Dimensions 2x and (2x-8): Variable Expression Problem Calculate Rectangle Area: Finding x(x-4) with Variable Dimensions Solve for X: Rectangle with Width 8cm and Area 32cm²

Characteristics and Proofs of a Rectangle

Verify Rectangle Properties: Number of Right Angles Analysis Rectangle ABCD: Proving Diagonal Equality in Quadrilaterals Rectangle ABCD: Are the Diagonals Perpendicular to Each Other? Rectangle ABCD: Do Diagonals Bisect Interior Angles? Rectangle Verification: Analyzing Quadrilateral ABCD Using Diagonal Properties

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Applying the formula A shape consisting of several shapes (requiring the same formula) Calculate The Missing Side based on the formula Calculation using the diagonal Extended distributive law Finding Area based off Perimeter and Vice Versa Subtraction or addition to a larger shape Using additional geometric shapes Using Pythagoras' theorem Using ratios for calculation Using short multiplication formulas Using variables Worded problems Drawing a rectangle based on properties Identifying and defining elements True / false

More Resources and Links

Explore more resources and links related to Rectangles for Ninth Grade
Practice From a Quadrilateral to a RectanglePractice From a Parallelogram to a RectanglePractice Diagonals in a rectangle