Simple Fractions - Examples, Exercises and Solutions

Practice FractionsPractice A fraction as a divisorPractice How do you simplify fractions?Practice Simplification and Expansion of Simple FractionsPractice Common denominatorPractice Part of a quantityPractice Placing Fractions on the Number LinePractice NumeratorPractice Denominator
Question Types:
Fractions as Divisors: Basic identificationFractions as Divisors: Worded problemsFractions as Divisors: Calculate the fractionFractions as Divisors: Writing the fractionPart of an Amount: Approximate the area of the colored part of the shapePart of an Amount: Identify the greater valuePart of an Amount: Visual representation of a fractionFractions as Divisors: Converting the fraction to digitsFractions as Divisors: Reducing the fractionFractions as Divisors: Using negative numbers

What are fractions?

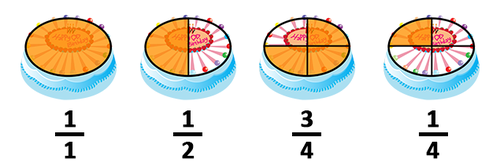
Fractions refer to the number of parts that equal the whole.

Suppose we have a cake divided into equal portions, the fraction comes to represent each of the portions into which we have cut the cake. Thus, if we have four equal portions, each of them represents a quarter of the pie. This is expressed numerically as follows: 141 \over 4.

The number 1 1 refers to the specific slice of the total pie set. We can look at it in the following way: we are talking about one slice and, therefore, we express it with a 1 1 . If we were talking about two slices, instead of 1 1 we would write 2 2 .

The number 4 4 refers to all equal portions of the pie. Since we have divided the pie into four equal portions, the number that should represent this division is 4 4 .

Cake visually divided

Detailed explanation

Practice Simple Fractions

Question 1

My numerator is 2 and my denominator is 9.

Which fraction am I?

Question 2

My numerator is 3 and my denominator is 8.

Which fraction am I?

Question 3

My numerator is 5 and my denominator is 8.

Which fraction am I?

Question 4

My numerator is 6 and my denominator is 7.

Which am I?

Question 5

My numerator is 8 and my denominator is 11.

Which fraction am I?

Examples with solutions for Simple Fractions

Exercise #1

My numerator is 2 and my denominator is 9.

Which fraction am I?

Video Solution

Step-by-Step Solution

Let's remember that the numerator is the number at the top of the fraction, whilst the denominator is the number at the bottom of the fraction.

If we arrange the given values accordingly we should obtain the following:

29 \frac{2}{9}

Answer

29 \frac{2}{9}

Exercise #2

My numerator is 3 and my denominator is 8.

Which fraction am I?

Video Solution

Step-by-Step Solution

Let's remember that the numerator is the number at the top of the fraction , whilst the denominator is the number at the bottom of the fraction.

If we insert the given values accordingly we should obtain the following:

38 \frac{3}{8}

Answer

38 \frac{3}{8}

Exercise #3

My numerator is 5 and my denominator is 8.

Which fraction am I?

Video Solution

Step-by-Step Solution

Remember that the numerator is the number at the top of the fraction, whilst the denominator is the number at the bottom of the fraction.

If we place the given values accordingly we should obtain the following:

58 \frac{5}{8}

Answer

58 \frac{5}{8}

Exercise #4

My numerator is 6 and my denominator is 7.

Which am I?

Step-by-Step Solution

Remember that the numerator of the fraction is the top half, whilst the denominator of the fraction is the bottom half.

If we position them accordingly we should obtain the following:

67 \frac{6}{7}

Answer

67 \frac{6}{7}

Exercise #5

My numerator is 8 and my denominator is 11.

Which fraction am I?

Video Solution

Step-by-Step Solution

Remember that the numerator is the number at the top of the fraction, whilst the denominator is the number at the bottom of the fraction.

If we arrange the given data accordingly we should obtain the following:

811 \frac{8}{11}

Answer

811 \frac{8}{11}

Question 1

Solve the following:

\( \frac{10}{5}= \)

Question 2

Solve the following:

\( \frac{13}{13}= \)

Question 3

Solve the following:

\( \frac{2}{18}= \)

Question 4

Solve the following:

\( \frac{29}{29}= \)

Question 5

Solve the following:

\( \frac{3}{4}= \)

Exercise #6

Solve the following:

105= \frac{10}{5}=

Step-by-Step Solution

First we will divide the numerator and denominator by the highest number that both are divisible by.

In this case, the number is 5.

Then we will divide the fraction as follows:

10:55:5=21=2 \frac{10:5}{5:5}=\frac{2}{1}=2

Answer

2 2

Exercise #7

Solve the following:

1313= \frac{13}{13}=

Step-by-Step Solution

First, we will divide the numerator and denominator by the highest number that both are divisible by.

In this case, the number is 13.

Then we will divide the fraction as follows:

13:1313:13=11=1 \frac{13:13}{13:13}=\frac{1}{1}=1

Answer

1 1

Exercise #8

Solve the following:

218= \frac{2}{18}=

Step-by-Step Solution

First we will divide the numerator and denominator by the highest number that both are divisible by.

In this case, the number is 2

Then we will divide the fraction as follows:

2:218:2=19 \frac{2:2}{18:2}=\frac{1}{9}

Answer

19 \frac{1}{9}

Exercise #9

Solve the following:

2929= \frac{29}{29}=

Step-by-Step Solution

First we will divide the numerator and denominator by the highest number that both are divisible by.

In this case, the number is 29.

Then we will divide the fraction as follows:

29:2929:29=11=1 \frac{29:29}{29:29}=\frac{1}{1}=1

Answer

1 1

Exercise #10

Solve the following:

34= \frac{3}{4}=

Step-by-Step Solution

We will divide the numerator and denominator by the highest number that both are divisible by.

In this case, there is no number by which we can divide, so the fraction will remain as it is.

Answer

34 \frac{3}{4}

Question 1

Solve the following:

\( \frac{56}{7}= \)

Question 2

Solve the following:

\( \frac{64}{8}= \)

Question 3

Solve the following:

\( \frac{-9}{9}= \)

Question 4

What fraction results from dividing 2 by 3?

Question 5

What fraction results from dividing 2 by 5?

Exercise #11

Solve the following:

567= \frac{56}{7}=

Step-by-Step Solution

First we will divide the numerator and denominator by the highest number that both are divisible by.

In this case, the number is 7.

Then we will divide the fraction as follows:

56:77:7=81=8 \frac{56:7}{7:7}=\frac{8}{1}=8

Answer

8 8

Exercise #12

Solve the following:

648= \frac{64}{8}=

Step-by-Step Solution

We will divide the numerator and denominator by the highest number that both are divisible by.

In this case, the number is 8

We will divide the fraction as follows:

64:88:8=81=8 \frac{64:8}{8:8}=\frac{8}{1}=8

Answer

8 8

Exercise #13

Solve the following:

−99= \frac{-9}{9}=

Step-by-Step Solution

Let's remember that we are dividing a positive number by a negative number, so the result will necessarily be a negative number.

We will divide both the numerator and the denominator by the highest number that both are divisible by.

In this case, the number is -9

We will divide the fraction as follows:

−9:−99:−9=1−1=−1 \frac{-9:-9}{9:-9}=\frac{1}{-1}=-1

Answer

−1 -1

Exercise #14

What fraction results from dividing 2 by 3?

Video Solution

Step-by-Step Solution

First, let's write the division exercise:

2:3 2:3

Now let's write it as a simple fraction, remembering that the numerator is on top and the denominator is on the bottom:

23 \frac{2}{3}

Answer

23 \frac{2}{3}

Exercise #15

What fraction results from dividing 2 by 5?

Video Solution

Step-by-Step Solution

Firstly, let's write out the division exercise:

2:5 2:5

Now, let's write it out again as a simple fraction, remembering that the numerator is on top and the denominator is on the bottom:

25 \frac{2}{5}

Answer

25 \frac{2}{5}

More Questions