Simplification and Expansion of Simple Fractions - Examples, Exercises and Solutions

Simplification and Expansiono f Simple Fractions

To amplify fractions

We will perform the same multiplication operation on the numerator and the denominator: the value of the fraction will be preserved.

You can expand as many times as you want and by any number.

To simplify fractions:

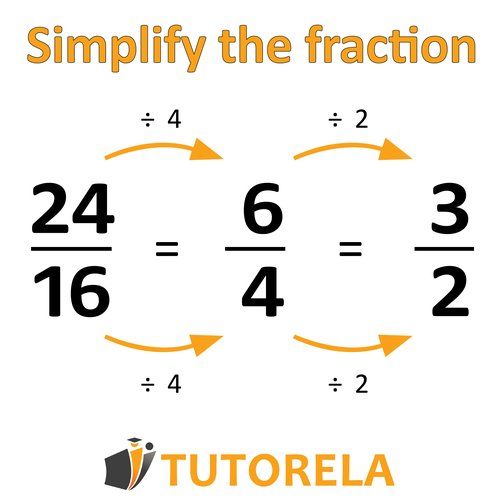
We will perform the same division operation on the numerator and the denominator: the value of the fraction will be preserved.

This can only be done with a number that is completely divisible by both the numerator and the denominator.

It is possible to simplify only until reaching a fraction in which it is not possible to find a number that divides without remainder both in the numerator and the denominator.

Practice Simplification and Expansion of Simple Fractions

Question 1

Simplify the following fraction by a factor of 4:

$\frac{4}{8}=$

Question 2

Simplify the following fraction by a factor of 1:

$\frac{3}{10}=$

Question 3

Simplify the following fraction:

$\frac{2}{10}=$

Question 4

Simplify the following fraction:

$\frac{4}{16}=$

Question 5

Simplify the following fraction by a factor of 3:

$\frac{3}{6}=$

Examples with solutions for Simplification and Expansion of Simple Fractions

Exercise #1

Simplify the following fraction by a factor of 4:

$\frac{4}{8}=$

Video Solution

Step-by-Step Solution

Let's simplify as follows, we'll divide both the numerator by 4 and the denominator by 4:

$\frac{4:4}{8:4}=\frac{1}{2}$

Answer

$\frac{1}{2}$

Exercise #2

Simplify the following fraction by a factor of 1:

$\frac{3}{10}=$

Video Solution

Step-by-Step Solution

We will reduce in the following way, divide the numerator by 1 and the denominator by 1:

$\frac{3:1}{10:1}=\frac{3}{10}$

Answer

$\frac{3}{10}$

Exercise #3

Simplify the following fraction:

$\frac{2}{10}=$

Video Solution

Step-by-Step Solution

Let's simplify as follows, we'll divide both the numerator by 2 and the denominator by 2:

$\frac{2:2}{10:2}=\frac{1}{5}$

Answer

$\frac{1}{5}$

Exercise #4

Simplify the following fraction:

$\frac{4}{16}=$

Video Solution

Step-by-Step Solution

We will reduce in the following way, divide the numerator by 4 and the denominator by 4:

$\frac{4:4}{16:4}=\frac{1}{4}$

Answer

$\frac{1}{4}$

Exercise #5

Simplify the following fraction by a factor of 3:

$\frac{3}{6}=$

Video Solution

Step-by-Step Solution

We will reduce as follows, divide the numerator by 3 and the denominator by 3:

$\frac{3:3}{6:3}=\frac{1}{2}$

Answer

$\frac{1}{2}$

Question 1

Simplify the following fraction:

$\frac{12}{8}=$

Question 2

Simplify the following fraction:

$\frac{1}{1}=$

Question 3

Simplify the following fraction by a factor of 5:

$\frac{15}{10}=$

Question 4

Simplify the following fraction:

$\frac{12}{4}=$

Question 5

Simplify the following fraction:

$\frac{16}{8}=$

Exercise #6

Simplify the following fraction:

$\frac{12}{8}=$

Video Solution

Step-by-Step Solution

Let's simplify as follows, we'll divide both the numerator by 2 and the denominator by 2:

$\frac{12:2}{8:2}=\frac{6}{4}$

Answer

$\frac{6}{4}$

Exercise #7

Simplify the following fraction:

$\frac{1}{1}=$

Video Solution

Step-by-Step Solution

Let's reduce as follows, we'll divide both the numerator and denominator by 1:

$\frac{1:1}{1:1}=\frac{1}{1}$

Answer

$\frac{1}{1}$

Exercise #8

Simplify the following fraction by a factor of 5:

$\frac{15}{10}=$

Video Solution

Step-by-Step Solution

Let's reduce as follows, we'll divide both the numerator and denominator by 5:

$\frac{15:5}{10:5}=\frac{3}{2}$

Answer

$\frac{3}{2}$

Exercise #9

Simplify the following fraction:

$\frac{12}{4}=$

Video Solution

Step-by-Step Solution

Let's reduce as follows, divide the numerator by 4 and the denominator by 4:

$\frac{12:4}{4:4}=\frac{3}{1}$

Answer

$\frac{3}{1}$

Exercise #10

Simplify the following fraction:

$\frac{16}{8}=$

Video Solution

Step-by-Step Solution

Let's simplify as follows, we'll divide both the numerator by 2 and the denominator by 2:

$\frac{16:2}{8:2}=\frac{8}{4}$

Answer

$\frac{8}{4}$

Question 1

Simplify the given fraction to the denominator 9:

$\frac{12}{18}=$

Question 2

Simplify the following fraction:

$\frac{6}{24}=$

Question 3

Simplify the given fraction to the denominator 12:

$\frac{6}{24}=$

Question 4

Simplify the given fraction to the denominator 10:

$\frac{5}{50}=$

Question 5

Simplify the following fraction and specify the simplification factor:

$\frac{16}{36}=$

Exercise #11

Simplify the given fraction to the denominator 9:

$\frac{12}{18}=$

Video Solution

Step-by-Step Solution

Let's look at the denominator of the fraction. We'll try to find a number that, when divided by 18, gives us a result of 9

Therefore:

$\frac{12:2}{18:2}=\frac{6}{9}$

Answer

$\frac{6}{9}$

Exercise #12

Simplify the following fraction:

$\frac{6}{24}=$

Video Solution

Step-by-Step Solution

Let's look at the denominator of the fraction. We'll try to find a number that, when divided by 24, gives us a result of 4

Therefore:

$\frac{6:6}{24:6}=\frac{1}{4}$

Answer

$\frac{1}{4}$

Exercise #13

Simplify the given fraction to the denominator 12:

$\frac{6}{24}=$

Video Solution

Step-by-Step Solution

Let's look at the denominator of the fraction. We'll try to find a number that, when divided by 24, gives us a result of 12

Therefore:

$\frac{6:2}{24:2}=\frac{3}{12}$

Answer

$\frac{3}{12}$

Exercise #14

Simplify the given fraction to the denominator 10:

$\frac{5}{50}=$

Video Solution

Step-by-Step Solution

Let's look at the denominator of the fraction. We'll try to find a number that, when divided by 50, gives us a result of 10

Therefore:

$\frac{5:5}{50:5}=\frac{1}{10}$

Answer

$\frac{1}{10}$

Exercise #15

Simplify the following fraction and specify the simplification factor:

$\frac{16}{36}=$

Video Solution

Step-by-Step Solution

Let's look at the denominator of the fraction. We'll try to find a number that, when divided by 36, gives us a result of 18

Therefore:

$\frac{16:2}{36:2}=\frac{8}{18}$

Answer

$\frac{8}{18}$ , factor of 2

Topics learned in later sections

Simplification and Expansion of Simple Fractions - Examples, Exercises and Solutions