Given the expression of the quadratic functionThe symmetrical axis of the expression must be found.$$ f(x)=-3x^2+3 $$

There is no axis of symmetry.

Given the expression of the quadratic functionThe symmetrical axis of the expression must be found.$$ f(x)=7x^2 $$

There is no axis of symmetry.

Given the expression of the quadratic functionFinding the symmetry point of the function$$ f(x)=\frac{1}{2}x^2 $$

$$ (\frac{1}{2},\frac{1}{2}) $$

Symmetry in a parabola

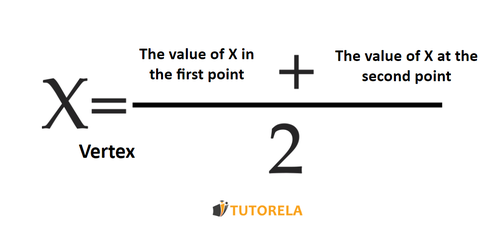
The axis of symmetry in a parabola is the axis that passes through its vertex in such a way that if we folded the right side over the left side, both sides would appear joined.
Let's see it in an illustration:

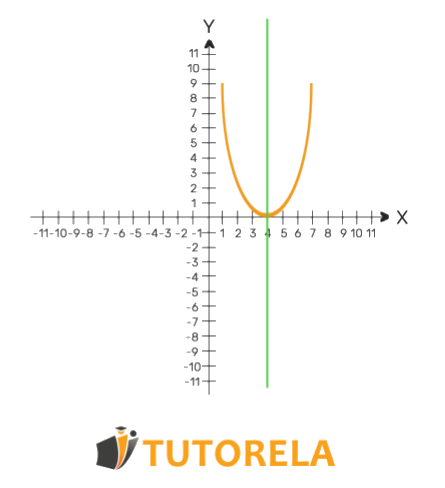
To find the axis of symmetry, we must locate the value of $X$ of the vertex of the parabola or do it through the parabola's vertex formula or with the help of two symmetric points on the parabola.

Vertex Formula of the Parabola

$X=\frac{-b}{2a}$

Formula for two symmetric points:

$X_{Vertex}=\frac{The~value~of~X~at~the~first~point~+~The~value~of~X~at~the~second~point}{2}$

Detailed explanation

Start practice

Test yourself on symmetry!

Given the expression of the quadratic function

The symmetrical axis of the expression must be found.

$$ f(x)=-3x^2+3 $$

Practice more now

Let's look at an example

First method: Solve for X at the vertex based on the formula.

Given the function $x^2+8x+5$
Let's plug it into the formula and we will get:
$x=-\frac{8}{2\cdot1}=-\frac{8}{1}=-8$
From this it follows that, the axis of symmetry is $X=-8$