Quadratic Equations System - Algebraic and Graphical Solution

🏆Practice systems of quadratic equations
5 Questions
Equations and Systems of Quadratic Equations
Systems of Quadratic Equations
Practice
Add a new subject

Quadratic Equations System

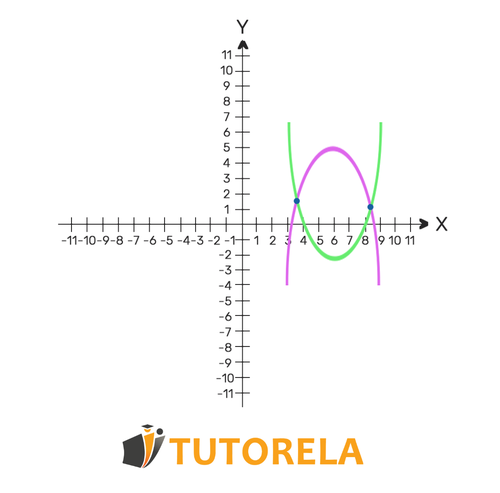
In the system of quadratic equations, we must find the XX and YY that satisfy the first equation as well as the second. The system can have one solution, two solutions, or even none. The concept of the solution of the system of equations highlights the points of intersection of the function. At the same points we find - the functions intersect. If one solution is found - the functions intersect once. If two solutions are found - the functions intersect twice. If no solution is found - the functions never intersect.

Start practice

Test yourself on systems of quadratic equations!

einstein

Consider the following relationships between the variables x and y:

\( x^2+4=-6y \)

\( y^2+9=-4x \)

Which answer is correct?

Practice more now

Algebraic solution

Method: Comparison between quadratic equations

When we have a system of quadratic equations and the YY is isolated in this way (with the same coefficient in both equations):
Y=ax2+bx+cY=ax^2+bx+c
Y=ax2+bx+cY=ax^2+bx+c

We will proceed in the following order:

  1. We will verify that the variable YY is written in the same way in both equations
  2. We will compare the equations 
  3. We will solve for the XXs
  4. We will gradually substitute XXs into one of the equations to solve for its YY
  5. We will neatly record the solutions we have found.

Attention - The other parameters do not necessarily have to be the same. Only the YY needs to be isolated in the same way in order to equate the equations.

Graphical solution

The solution of the system of quadratic equations represents the points of intersection of the parabolas. Therefore, we will be able to see the solution of the system of equations graphically as the points of intersection of the parabolas.

Join Over 30,000 Students Excelling in Math!
Endless Practice, Expert Guidance - Elevate Your Math Skills Today
Test your knowledge
Question 1

Look at the rectangle in the figure.

\( x>0 \)

The area of the rectangle is:

\( x^2-13 \).

Calculate x.

x-4x-4x-4x+1x+1x+1x²-13

Question 2

\( \begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0 \)

Solve the above equations by completing the square/ factoring:

Make sure to explain the steps , and show your work: , including all calculations:

\( (a+by)^2(a-by)=\text{?} \)


Question 3

Consider the following relationships between the variables x and y:

\( x^2+4=-6y \)

\( y^2+9=-4x \)

Which answer is correct?

If a solution is found - the functions intersect only once

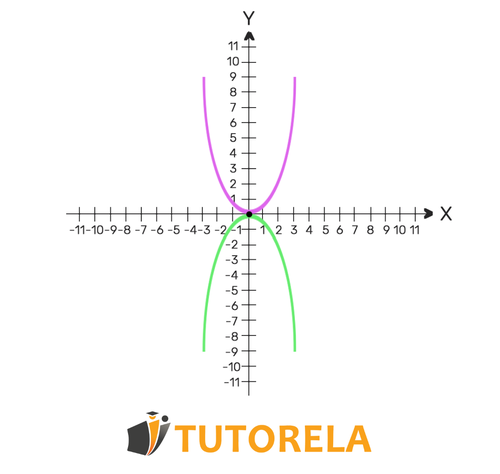
1a- Graphic solution

If two solutions are found - the functions intersect twice

2a - If two solutions are found

Do you know what the answer is?
Question 1

Look at the rectangle in the figure.

\( x>0 \)

The area of the rectangle is:

\( x^2-13 \).

Calculate x.

x-4x-4x-4x+1x+1x+1x²-13

Question 2

\( \begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0 \)

Solve the above equations by completing the square/ factoring:

Make sure to explain the steps , and show your work: , including all calculations:

\( (a+by)^2(a-by)=\text{?} \)


Question 3

Consider the following relationships between the variables x and y:

\( x^2+4=-6y \)

\( y^2+9=-4x \)

Which answer is correct?

If no solution is found - the functions never intersect

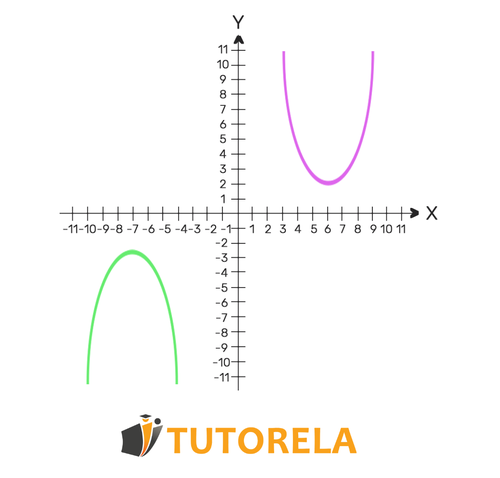
3a - If no solution is found

Let's look at an example

y=5x2−2x+6y=5x^2-2x+6
y=−5x2−2x+6y=-5x^2-2x+6

  1. Let's verify that the YY is really isolated in the same way.
  2. Let's compare the equations:
    5x2−2x+6=−5x2−2x+65x^2-2x+6=-5x^2-2x+6
  3. Let's solve for XXs
    5x2−2x+6=−5x2−2x+65x^2-2x+6=-5x^2-2x+6
    Let's transpose terms and we will get:
    10x2=010x^2=0
    x2=0x^2=0
    x=0x=0
  4. Let's find the YY by substituting the XX we found into one of the equations:
    y=5x2−2x+6y=5x^2-2x+6
    y=5∗02−2∗0+6y=5*0^2-2*0+6
    y=6y=6
  5. Let's note the solution we found: (6,0)(6, 0)
    at this point the functions intersect and that is the solution to the system of equations.

If you are interested in this article, you may also be interested in the following articles:

The functions y=x²

Family of parabolas y=x²+c: Vertical shift

Family of parabolas y=(x-p)²

Family of parabolas y=(x-p)²+k (combination of horizontal and vertical shift)

Vertex form of the quadratic function

Factored form of the quadratic function

Completing the square in a quadratic equation

Standard form of the quadratic function

Solution of a system of equations when one is linear and the other quadratic

In the blog of Tutorela you will find a variety of articles about mathematics.

Examples and exercises with solutions of quadratic equation systems

Exercise #1

Look at the rectangle in the figure.

x>0

The area of the rectangle is:

x2−13 x^2-13 .

Calculate x.

x-4x-4x-4x+1x+1x+1x²-13

Video Solution

Step-by-Step Solution

First, let's recall the formula for calculating the area of a rectangle:

The area of a rectangle (which has two pairs of equal opposite sides and all angles are 90° 90\degree ) with sides of length a,b a,\hspace{4pt} b units, is given by the formula:

S=a⋅b \boxed{ S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=a\cdot b } (square units)

90°90°90°bbbaaabbbaaa

After recalling the formula for the area of a rectangle, let's solve the problem:

First, let's denote the area of the given rectangle as: S S_{\textcolor{blue}{\boxed{\hspace{6pt}}}} and write (in mathematical notation) the given information:

S=x2−13 S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=x^2-13

Let's continue and calculate the area of the rectangle given in the problem:

x-4x-4x-4x+1x+1x+1x²-13

Using the rectangle area formula mentioned earlier:

S=a⋅b↓S=(x−4)(x+1) S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=a\cdot b\\ \downarrow\\ S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=(x-4)(x+1)

Let's continue and simplify the expression we got for the rectangle's area, using the distributive property:

(c+d)(h+g)=ch+cg+dh+dg (c+d)(h+g)=ch+cg+dh+dg

Therefore, we get that the area of the rectangle by

using the distributive property is:

S=(x−4)(x+1)S=x2+x−4x−4S=x2−3x−4 S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=(x-4)(x+1) \\ S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=x^2+x-4x-4\\ \boxed{ S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=x^2-3x-4}

Now let's recall the given information:

S=x2−13 S_{\textcolor{blue}{\boxed{\hspace{6pt}}}}=x^2-13

Therefore, we can conclude that:

x2−3x−4=x2−13↓−3x=4−13−3x=−9/(−3)x=3 x^2-3x-4=x^2-13 \\ \downarrow\\ -3x=4-13\\ -3x=-9\hspace{6pt}\text{/}(-3)\\ \boxed{x=3}

We solved the resulting equation simply by combining like terms, isolating the expression with the unknown on one side and dividing both sides by the unknown's coefficient in the final step,

Note that this result satisfies the domain of definition for x, which was given as:

-1\text{<}x\text{<}4 and therefore it is the correct result

Therefore, the correct answer is answer C.

Answer

x=3 x=3

Exercise #2

Consider the following relationships between the variables x and y:

x2+4=−6y x^2+4=-6y

y2+9=−4x y^2+9=-4x

Which answer is correct?

Video Solution

Answer

(x+2)2+(y+3)2=0 (x+2)^2+(y+3)^2=0

Check your understanding
Question 1

Look at the rectangle in the figure.

\( x>0 \)

The area of the rectangle is:

\( x^2-13 \).

Calculate x.

x-4x-4x-4x+1x+1x+1x²-13

Question 2

\( \begin{cases} a^2x^3+2abx^2y=-2a(ax+by)\\ a(x+1)=-by \end{cases} \)\( b\neq0 ,\hspace{4pt}a\neq0 \)

Solve the above equations by completing the square/ factoring:

Make sure to explain the steps , and show your work: , including all calculations:

\( (a+by)^2(a-by)=\text{?} \)


Question 3

Consider the following relationships between the variables x and y:

\( x^2+4=-6y \)

\( y^2+9=-4x \)

Which answer is correct?

Start practice
Related Subjects
👉  Click here  to practice