Quadratic Inequality

The quadratic inequality shows us in which interval the function is positive and in which it is negative - according to the inequality symbol. To solve quadratic inequalities correctly, it is convenient to remember two things:

Set of positivity and negativity of the function:
Set of positivity - represents the $X$ s in which the graph of the parabola is above the $X$ axis, with $Y$ value positive.
Set of negativity - represents the $X$ s in which the graph of the parabola is below the $X$ axis, with $Y$ value negative.
Dividing by a negative term - reverses the sign of the inequality.

Method to solve the quadratic inequality:

We will carry out the transposition of members and isolate the quadratic equation until one side equals 0. Remember that when we divide by a negative term, the inequality is reversed.
Let's draw a diagram of the parabola - placing points of intersection with the $X$ axis and identifying the maximum and minimum of the parabola.
Let's calculate the corresponding interval according to the exercise and the diagram.
Quadratic equation $>0∶$ Set of positivity
Quadratic equation $<0∶$ Set of negativity

Detailed explanation

Start practice

Test yourself on quadratic inequalities!

Solve the following equation:

$$ x^2+4>0 $$

Practice more now

Let's look at an example of a quadratic inequality

$3x(x+1)<2(x^2+15)+2x$

Solution:
We will progress step by step:

1) Let's transpose terms and isolate the quadratic equation until one side equals $0$ . Remember that when we divide by a negative term, the inequality is reversed.
In the first step, we will leave $0$ on one side of the equation.
Note that, in this exercise, we must first solve what appears between parentheses.
We will open the parentheses and obtain:
$3x^2+3x>2x^2+30+2x$

Now let's transpose terms and we will obtain:
$X^2+X-30>0$

Magnificent. We have left $0$ on one side. Let's continue to the second step.

2) Let's draw a diagram of the parabola - placing intersection points with the $X$ axis and identifying the maximum and minimum of the parabola.

Let's find the intersection points of the function with the $X$ axis:
According to the quadratic formula we will obtain:

$X=5,-6$

We will see that the extremity of the function is the minimum (smile) since the coefficient of $X^2$ is positive.
Let's draw a diagram:

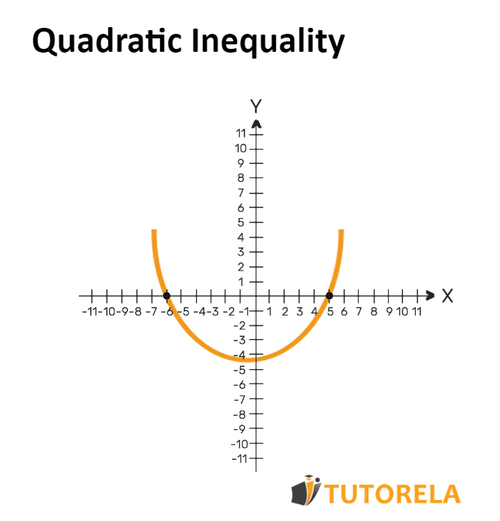
3) Let's calculate the corresponding interval according to the exercise and the diagram.
In the exercise, we arrived at the following equation:
$X^2+X-30>0$
That is, we are looking for the intervals in which the function is greater than $0$ . Its set of positivity.

We will ask ourselves: In which intervals is the function positive? At which $X$ s is the graph of the function above the $X$ axis?
The answer is when
$X>5$
$X<-6$