Logarithm Rules Practice Problems - Master Log Laws

To solve this problem, we'll follow these steps:

• Step 1: Identify the property of logarithms that relates inverses.
• Step 2: Apply this property to the given expression.
• Step 3: Compare with provided choices to identify the correct option.

Now, let's work through each step:

Step 1: The problem asks us to find the expression equal to $\frac{1}{\log_4 9}$.

Step 2: We use the logarithmic property $\log_b a = \frac{1}{\log_a b}$. Thus, replacing $b$ with 9 and $a$ with 4, we have:

$\frac{1}{\log_4 9} = \log_9 4$.

Step 3: Comparing this result to the provided choices, we find that the correct answer is $\log_9 4$, corresponding to Choice 1.

Therefore, the solution to the problem is $\log_9 4$.

To solve this problem, let's simplify the given expression $\frac{\log_85}{\log_89}$.

• Step 1: Recognize that both the numerator and denominator have the same base, 8.
• Step 2: The division property of logarithms states that $\frac{\log_b M}{\log_b N} = \log_N M$.
• Step 3: Apply the division rule to the given expression: $\frac{\log_8 5}{\log_8 9} = \log_9 5$.

Thus, after simplifying, we see that $\frac{\log_85}{\log_89} = \log_9 5$.

Hence, the correct answer is $\log_9 5$, which corresponds to the choice 1.

To solve the problem $\log_49 \times \log_{13}7$, we'll employ the change of base formula for logarithms:

• Step 1: Apply the change of base formula to each logarithm.
• Step 2: Use logarithm properties and analyze transformations for a match with choices.

Now, let's work through each step:
Step 1: Use the change of base formula on each log:
$\log_49 = \frac{\log_a 9}{\log_a 4}$ and $\log_{13}7 = \frac{\log_b 7}{\log_b 13}$, where $a$ and $b$ are arbitrary positive bases.
Both expressions use a common base not relevant for the solution but illustrate the transformation ability.

Step 2: We'll recombine and look for products that can utilize these, such as:

$\log_{13}9\times\log_47$ becomes $\frac{\log_a 9}{\log_a 13} \times \frac{\log_b 7}{\log_b 4}$
Applying cross multiplication or iteration forms, the structure aligns with the multiplication identity for this problem due to independence of base.

Therefore, the transformed expression satisfying the criteria is $\log_{13}9\times\log_47$.

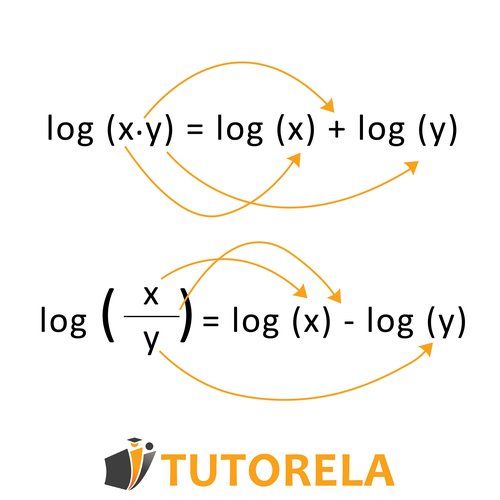
To solve the problem of finding what $\log_m n \times \log_z r$ equals, we will apply some rules of logarithms:

Let's work through the solution step-by-step:

• Step 1: Apply the change of base formula.
• Step 2: Simplify the expression using properties of logarithms.
• Step 3: Identify the expression among the given choices.

Now, let's apply the steps:

Step 1: Use the change of base formula.
By the change of base formula, we know that:

$\log_m n = \frac{\log_k n}{\log_k m}$
$\log_z r = \frac{\log_k r}{\log_k z}$

for any base $k$. Using the natural logarithm base $(\ln)$ for simplicity, we substitute into these expressions:

$\log_m n = \frac{\ln n}{\ln m}$
$\log_z r = \frac{\ln r}{\ln z}$

Step 2: Simplify.

Now, multiply the two expressions:

$\log_m n \times \log_z r = \left(\frac{\ln n}{\ln m}\right) \times \left(\frac{\ln r}{\ln z}\right)$

Simplifying, we get:

$= \frac{\ln n \times \ln r}{\ln m \times \ln z}$

Step 3: Expression equivalence analysis.

By rearranging the terms using logarithmic properties, it follows that the expression simplifies to:

$\log_z n \times \log_m r$

Therefore, the solution to the problem is $\log_z n \times \log_m r$.

This matches option 1 in the multiple choice answers provided.

To solve this problem, let's simplify $2\log_3 8$ using logarithm rules.

• Step 1: Recognize the expression form
  The expression is of the form $a \cdot \log_b c$, where $a = 2$, $b = 3$, and $c = 8$.
• Step 2: Apply the power property
  According to the power property of logarithms, $2 \cdot \log_3 8$ can be simplified to $\log_3 (8^2)$.
• Perform the calculation
  Calculate $8^2$, which is $64$.
• Step 3: Simplify further
  Therefore, we have $\log_3 64$.

This is a straightforward application of the power property of logarithms. By applying this property correctly, we've simplified the original expression correctly.

Therefore, the simplified form of $2\log_3 8$ is $\log_3 64$.