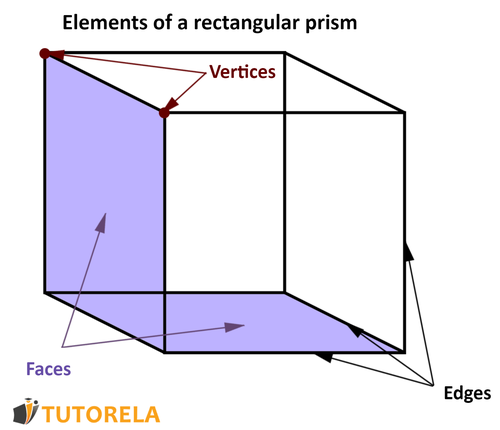
The rectangular cuboid, or just cuboid, is a three-dimensional shape that consists of six rectangles. Each rectangle is called a face. Every rectangular cuboid has six faces (The top and bottom faces are often called the top and bottom bases of the rectangular cuboid). It is important to understand that there are actually pairs of faces, and each face will be identical to its opposite face.
The straight lines formed by two intersecting sides are called edges (or sides). Every cuboid has edges.
The meeting point between two edges is called the vertex. Each cuboid has vertices.